
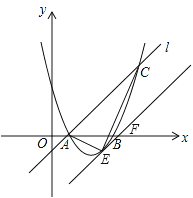
����Ŀ����ͼ����֪������y=ax2+bx+3��x�ύ��A��B���㣬����A��ֱ��l�������߽��ڵ�C������A��������ǣ�1��0����C�������ǣ�4��3����

��1���������ߵĽ���ʽ��
��2���ڣ�1���������ߵĶԳ������Ƿ���ڵ�D��ʹ��BCD���ܳ���С�������ڣ������D�����꣬�������ڣ���˵�����ɣ�
��3������E�ǣ�1�����������ϵ�һ�����㣬��λ��ֱ��AC���·���������ACE����������E������꣮
���𰸡��⣺��1����������y=ax2+bx+3������A��1��0������C��4��3����
��![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy=x2��4x+3��
��2�����ڡ�
����A��B���ڶԳ���Գƣ�����DΪAC��Գ���Ľ���ʱ��BCD���ܳ���С��
��y=x2��4x+3=��x��2��2��1���������ߵĶԳ���Ϊֱ��x=2��
��ֱ��AC�Ľ���ʽΪy=kx+b��k��0����
��![]() ����ã�
����ã�![]() ��
��
��ֱ��AC�Ľ���ʽΪy=x��1��
��x=2ʱ��y=2��1=1��
�������߶Գ����ϴ��ڵ�D��2��1����ʹ��BCD���ܳ���С��
��3����ͼ�������E��ֱ��ACƽ���ߵ�ֱ��Ϊy=x+m��
����![]() ������y�ã�x2��5x+3��m=0��
������y�ã�x2��5x+3��m=0��
����=����5��2��4��1����3��m��=0��m=![]() ��
��
��m=![]() ʱ����E��AC�ľ��������ACE��������
ʱ����E��AC�ľ��������ACE��������
��ʱx=![]() ��y=
��y=![]() ��
��
����E��������![]() ��
��![]() ����
����
�����E��ֱ����x�ύ��ΪF����F��![]() ��0����
��0����
��AF=![]() ��
��
��ֱ��AC�Ľ���ʽΪy=x��1�����CAB=45����
����F��AC�ľ���Ϊ![]() ��
��
����![]() ��
��
���ACE��������![]() ����ʱE������Ϊ��
����ʱE������Ϊ��![]() ��
��![]() ����
����
��������
���⣨1�����ô���ϵ��������κ�������ʽ��ɡ�
��2�����ô���ϵ�������ֱ��AC�Ľ���ʽ��Ȼ�������Գ�ȷ�����·�����⣬ֱ��AC��Գ���Ľ��㼴Ϊ�����D��
��3������ֱ��AC�Ľ���ʽ���������E��ACƽ�е�ֱ�ߣ�Ȼ���������߽���ʽ��������y�õ�����x��һԪ���η��̣����ø����б�ʽ��=0ʱ����ACE��������Ȼ�������ʱ��ACƽ�е�ֱ�ߣ�Ȼ�������E�����꣬�������ֱ����x��Ľ���F�����꣬�����AF���ٸ���ֱ��l��x��ļн�Ϊ45�������ֱ��ľ��룬�����AC��ľ��룬Ȼ�����������ε������ʽ��ʽ���㼴�ɵý⡣


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪�����ٷ������Ի�Ϊ������������ĺ͵���ʽ�����磺![]() .
.
�ڷ�ʽ�У�����ֻ����һ����ĸ�ķ�ʽ�������ӵĴ������ڻ���ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ���ٷ�ʽ���������ӵĴ���С�ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ�����ʽ��.
���磺��![]() ��
��![]() ���������ķ�ʽ�Ǽٷ�ʽ����
���������ķ�ʽ�Ǽٷ�ʽ����![]() ��
��![]() ���������ķ�ʽ�����ʽ.
���������ķ�ʽ�����ʽ.
���Ƶģ��ٷ�ʽҲ���Ի�Ϊ��ʽ�����ʽ�ĺͣ������ʽ.
���磺����ʽ![]() ��ֳ�һ����ʽ��һ�����ʽ�ĺͣ������ʽ.
��ֳ�һ����ʽ��һ�����ʽ�ĺͣ������ʽ.
����һ���⣺�ɷ�ĸΪ![]() ������
������![]()
����![]()
��������![]() ��������ʽ��������
��������ʽ��������
��![]() �����
�����![]()
��![]()
��������ʽ![]() �ͱ���ֳ�һ����ʽ��һ�����ʽ�ĺͣ������ʽ.
�ͱ���ֳ�һ����ʽ��һ�����ʽ�ĺͣ������ʽ.
���������⣺
![]()
��������ʽ![]() �Ͳ�ֳ�һ����ʽ��һ�����ʽ�ĺͣ������ʽ.
�Ͳ�ֳ�һ����ʽ��һ�����ʽ�ĺͣ������ʽ.
��1�����������ķ�����ѡ������һ�ַ�������ʽ![]() ��ֳ�һ����ʽ��һ�����ʽ�ĺͣ������ʽ��
��ֳ�һ����ʽ��һ�����ʽ�ĺͣ������ʽ��
��2����֪����![]() ʹ��ʽ
ʹ��ʽ![]() ��ֵΪ���������������������������
��ֵΪ���������������������������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӱ߳�Ϊa���������м���һ���߳�Ϊb��������(��ͼ��),Ȼ��ʣ�ಿ��ƴ��һ��������(��ͼ��).

(1) ������������֤�ĵ�ʽ��__________________;
(2) Ӧ�����(1)�ó��ĵ�ʽ��������и��⣺
����֪x24y2=12��x+2y=4����x2y��ֵ.
�����㣺(1![]() )(1
)(1![]() )(1
)(1![]() )��(1
)��(1![]() )(1
)(1![]() ).
).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ����֮����һ��270ǧ�Ĺ�·���ס�������ͬʱ�������׳���ÿСʱ60ǧ��/ʱ���ٶ��ش˹�·��
����֮����һ��270ǧ�Ĺ�·���ס�������ͬʱ�������׳���ÿСʱ60ǧ��/ʱ���ٶ��ش˹�·��![]() �����ٿ���
�����ٿ���![]() �أ��ҳ���
�أ��ҳ���![]() ���ش˹�·���ٿ���
���ش˹�·���ٿ���![]() �أ������ֱ�Ŀ�ĵغ�ֹͣ�ס�����������·��
�أ������ֱ�Ŀ�ĵغ�ֹͣ�ס�����������·��![]() (ǧ��)��׳�����ʻʱ��
(ǧ��)��׳�����ʻʱ��![]() (ʱ)֮��ĺ�����ϵ��ͼ��ʾ��
(ʱ)֮��ĺ�����ϵ��ͼ��ʾ��

(1)������ٶ�Ϊ______ǧ��/ʱ��![]() _____��
_____��![]() ______.
______.
(2)��ס�������������![]() ��
��![]() ֮��ĺ�����ϵʽ����д����Ӧ���Ա���
֮��ĺ�����ϵʽ����д����Ӧ���Ա���![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y��![]() x2��4x��7��y��
x2��4x��7��y��![]() x����A��B����(��A�ڵ�B���)��
x����A��B����(��A�ڵ�B���)��
(1)��A��B�������ꣻ
(2)�������߶���C�������������ABC�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵ���ֱ��������![]() �У�
��![]() ,��
,��![]() ��
��![]() ���ϣ�����
���ϣ�����![]() ������
������![]()

��1����֤��![]()
��2����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() ������
������![]()
�ٲ�ȫͼ�β�֤��![]()
�����ñ���ͼ���л�ͼ�����顢̽�����ҳ���![]() ����ǡ�ù���ʱ��
����ǡ�ù���ʱ��![]() ��λ�ã���ֱ��д����ʱ
��λ�ã���ֱ��д����ʱ![]() �Ķ�������������Ӧ��ͼ��
�Ķ�������������Ӧ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������
������![]() �͵�
�͵�![]() ����
����![]() ��
��

![]() ��ͼ����
��ͼ����![]() ��ǡ���������ߵĶ��㣬��д�����ĶԳ����
��ǡ���������ߵĶ��㣬��д�����ĶԳ����![]() ��ֵ��
��ֵ��
![]() ��
��![]() ����
����![]() ��
��![]() ��ֵ����ָ����ʱ�����ߵĿ��ڷ���
��ֵ����ָ����ʱ�����ߵĿ��ڷ���
![]() ��������
��������![]() �Ŀ������£���ֱ��д��
�Ŀ������£���ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˽���������Ϸ������������״��С��ȫ��ͬ���ƣ�����ֱ��������1��2��3��4���������Ʊ��泯�ϣ�ϴ�Ⱥ���������ϡ��״��������ȡһ���ƣ���¼���ֺ�Ż�ϴ�ȣ����������ȡһ�š�
��1�������б�������״ͼ�ķ����������˳�ȡ��ͬ���ֵĸ��ʣ�
��2�������˳�ȡ�����ֲ�ľ���ֵ����1�����ʤ������ȡ�����ֲ�ľ���ֵ����1�����һ�ʤ�������Ϸ��ƽ��?���ø��ʵ�֪ʶ���Խ��͡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y��ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x����1�������ĸ����ۣ���c��0������B����![]() ��y1����C����
��y1����C����![]() ��y2��Ϊͼ���ϵ����㣬��y1��y2����2a��b��0����
��y2��Ϊͼ���ϵ����㣬��y1��y2����2a��b��0����![]() ��0��������ȷ�Ľ�����_____��
��0��������ȷ�Ľ�����_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com