
解:(1)由题意,得

解得

∴矩形的长为4,宽为3;
(2)在Rt△PAB中

,
∴
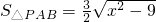
由矩形ABCD得AD∥BC?∠1=∠2,∠A=90°
又∵BC是半圆的直径得∠BQC=90°
∴∠A=∠BQC
∴△PAB∽△BQC

自变量x的取值范围是:3<x<5.
(3)当S
△BQC最大时,BC边上的高最大,此时Q点为半圆弧的中点.
∴QB=QC.
由(2)知:△PAB∽△BQC,∴AP=AB=3.
此时,PB=

=3

,即当S
△BQC最大时,

.
分析:(1)根据非负数的性质:两个非负数的和是0,因而两个非负数同时等于0,即可求得a,b的值;
(2)证得△PAB∽△BQC,根据相似三角形面积的比等于相似比的平方,即可求解;
(3)当S
△BQC最大时,BC边上的高最大,此时Q点为半圆弧的中点,在根据勾股定理即可求得PB的长.
点评:本题主要考查了矩形的性质,矩形的判定,相似三角形的判定和性质以及一次函数的综合应用.

 范围;
范围; 解:(1)由题意,得
解:(1)由题意,得

 ,
,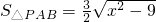

 =3
=3 ,即当S△BQC最大时,
,即当S△BQC最大时, .
.
