
|
|
|
|
|


科目:初中数学 来源: 题型:
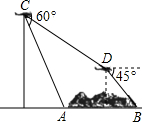 (2013•黄冈模拟)为了利用开发海洋资源,某勘测飞机欲测量一岛屿的两端A、B的距离,飞机在距海平面垂直高度300米的C处测得端点A的俯角为60°,然后飞机沿着俯角30°的方向俯冲到D点,发现端点B的俯角为45°,而此时飞机距离海平面的垂直高度为100米,求岛屿两端A、B的距离.(结果精确到0.1米,
(2013•黄冈模拟)为了利用开发海洋资源,某勘测飞机欲测量一岛屿的两端A、B的距离,飞机在距海平面垂直高度300米的C处测得端点A的俯角为60°,然后飞机沿着俯角30°的方向俯冲到D点,发现端点B的俯角为45°,而此时飞机距离海平面的垂直高度为100米,求岛屿两端A、B的距离.(结果精确到0.1米,| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•黄冈)钓鱼岛自古就是中国领土,中国政府已对钓鱼岛开展常态化巡逻.某天,为按计划准点到达指定海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是
(2013•黄冈)钓鱼岛自古就是中国领土,中国政府已对钓鱼岛开展常态化巡逻.某天,为按计划准点到达指定海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com