
【题目】(1)如图,分别把两个边长为![]() 的小正方形沿一条对角线裁成
的小正方形沿一条对角线裁成![]() 个小三角形拼成一个大正方形,则大正方形的边长为_______
个小三角形拼成一个大正方形,则大正方形的边长为_______![]() ;
;

(2)若一个圆的面积与一个正方形的面积都是![]() ,设圆的周长为
,设圆的周长为![]() ,正方形的周长为
,正方形的周长为![]() ,则
,则![]() _____
_____![]() (填“
(填“![]() ”或“
”或“![]() ”或“
”或“![]() ”号);
”号);
(3)如图,若正方形的面积为![]() ,李明同学想沿这块正方形边的方向裁出一块面积为
,李明同学想沿这块正方形边的方向裁出一块面积为![]() 的长方形纸片,使它的长和宽之比为
的长方形纸片,使它的长和宽之比为![]() ,他能裁出吗?请说明理由?
,他能裁出吗?请说明理由?

【答案】(1)![]() ;(2)
;(2)![]() ;(3)不能裁剪出,详见解析
;(3)不能裁剪出,详见解析
【解析】
(1)根据所拼成的大正方形的面积为2即可求得大正方形的边长;
(2)由圆和正方形的面积公式可分别求的圆的半径及正方形的边长,进而可求得圆和正方形的周长,利用作商法比较这两数大小即可;
(3)利用方程思想求出长方形的长边,与正方形边长比较大小即可;
解:(1)∵小正方形的边长为1cm,
∴小正方形的面积为1cm2,
∴两个小正方形的面积之和为2cm2,
即所拼成的大正方形的面积为2 cm2,
∴大正方形的边长为![]() cm,
cm,
(2)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设正方形的边长为a
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
故答案为:<;
(3)解:不能裁剪出,理由如下:
∵长方形纸片的长和宽之比为![]() ,
,
∴设长方形纸片的长为![]() ,宽为
,宽为![]() ,
,
则![]() ,
,
整理得:![]() ,
,
∴![]() ,
,
∵450>400,
∴![]() ,
,
∴![]() ,
,
∴长方形纸片的长大于正方形的边长,
∴不能裁出这样的长方形纸片.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的,该市自来水收费价格见价目表.
价目表
每月水用量 | 单价 |
不超出 |
|
超出 |
|
超出 |
|
注:水费按月结算.
若某户居民![]() 月份用水
月份用水![]() ,则应收水费:
,则应收水费:![]() 元.
元.
(1)若该户居民![]() 月份用水
月份用水![]() ,则应收水费_______元;
,则应收水费_______元;
(2)若该户居民![]() 、
、![]() 月份共用水
月份共用水![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份),共交水费
月份),共交水费![]() 元,则该户居民
元,则该户居民![]() 月份各用水多少立方米?
月份各用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:![]() =
=![]() (a≠0),即a的负P次幂等于a的p次幂的倒数.例:
(a≠0),即a的负P次幂等于a的p次幂的倒数.例:![]() =
=![]()
(1)计算:![]() =__;
=__;![]() =__;
=__;
(2)如果![]() =
=![]() ,那么p=__;如果
,那么p=__;如果![]() =
=![]() ,那么a=__;
,那么a=__;
(3)如果![]() =
=![]() ,且a、p为整数,求满足条件的a、p的取值.
,且a、p为整数,求满足条件的a、p的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表, 
请回答下列问题:
七年级兴趣班报名情况统计表.
兴趣班名称 | 频率 |
“无人机” | a |
“3D打印” | 0.05 |
“网页设计” | 0.25 |
“电脑绘画” | 0.40 |
(1)报名参加兴趣班的总人数为人;统计表中的a=;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
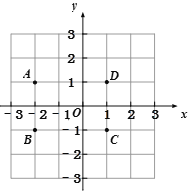
【题目】如图,点C的坐标是1,1,那么点A、B、D的坐标分别为:A(______), _____),B(______), _____),D(______), _____).其中,横坐标相等的点有______和_____,_____和_____.A、B、C、D四个点组成的图形是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣ ![]() x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2. 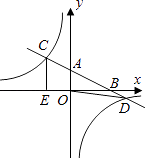
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com