
【题目】如图,平行四边形ABCD中,点P为CB延长线上点,连接DP交AC于点M、交AB于点N,已知DA=DC,∠ACD=45°.
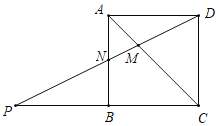
(1)求证:四边形ABCD为正方形;
(2)连接BM,若N为AB的中点,求tan∠BMP的值;
(3)若MN=2,PN=6,求DM的长.
【答案】(1)见解析;(2)![]() ;(3)4
;(3)4
【解析】
(1)有1个角为90°的菱形为正方形.
(2)证明△BPN≌△AND,然后用相似三角形性质求解
(3)MD2=MNMP
(1)证明:∵四边形ABCD是平行四边形,DA=DC,
∴四边形ABCD是菱形,
∵DA=DC,
∴∠ACD=∠CAD=45°,
∴∠ADC=90°,
∴四边形ABCD为正方形;
(2)解:作BE⊥PD,如图所示:
则∠PEB=∠MEB=90°,
设正方形ABCD的边长为a,
∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AB=AD=a,∠PBN=∠DAB=∠BCD=90°,
∵N为AB的中点,
∴AN=BN=![]() AB=
AB=![]() a,
a,
在△BPN和△ADN中, ,
,
∴△BPN≌△ADN(ASA),
∴BP=AD=a,PN=DN=![]() =
= =
=![]() a,PC=BP+BC=2a,
a,PC=BP+BC=2a,
∴PD=2DN=![]() a,
a,
∵AD∥BC,
∴△ADM∽△CPM,
∴![]() ,
,
∴![]() ,
,
∵∠PEB=∠PCD=90°,∠P=∠P,
∴△PBE∽△PDC,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴![]()
∴![]()
(3)解:MN=2,PN=6,
∴MP=8,
∵AB∥CD,
∴AM:MC=MN:MD,
∵AD∥BC,
∴AM:MC=DM:MP,
∴MN:MD=DM:MP,
∴MD2=MNMP=2×8=16,
∴MD=4.



科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象G经过点A(4,1),直线l:y=
(x>0)的图象G经过点A(4,1),直线l:y=![]() +b与图象G交于点B,与y轴交于点C.
+b与图象G交于点B,与y轴交于点C.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,B之间的部分与线段OA,OC,BC围成的区域(不含边界)为W.
①当b=﹣1时,直接写出区域W内的整点个数;
②若区域W内恰有4个整点,结合函数图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
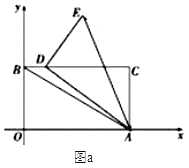
【题目】在平面直角坐标系中,矩形AOBC的顶点O与原点重合,A(10,0),B(0,6),以点A为中心顺时针旋转△BOA,得到△EDA,点B,O,A的对应点分别为E,D,A.
(1)如图a,当点D落在BC边上时,点D的坐标为______.
(2)如图b,当点B、D、E三点共线时,AD与BC交于点H.求点H的坐标;
(3)在△BOA旋转的过程中,M点为线段CA上中点,△DEM面积S的取值范围为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,以
两点,以![]() 为边长在第一象限内作正方形
为边长在第一象限内作正方形![]() ,若反比例函数
,若反比例函数![]() (
(![]() )的图象经过顶点
)的图象经过顶点![]() .
.
(1)试确定![]() 的值;
的值;
(2)若正方形![]() 向左平移
向左平移![]() 个单位后,顶点
个单位后,顶点![]() 恰好落在反比例函数
恰好落在反比例函数![]() 的图象上,试确定
的图象上,试确定![]() 的值.
的值.
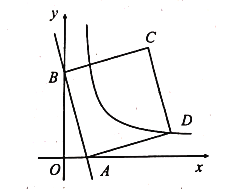
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1的顶点在y轴上,y2由y1平移得到,它们与x轴的交点为A、B、C,且2BC=3AB=4OD=6,若过原点的直线被抛物线y1、y2所截得的线段长相等,则这条直线的解析式为____________.
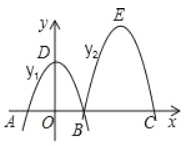
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园安全受到全社会的广泛关注,某市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
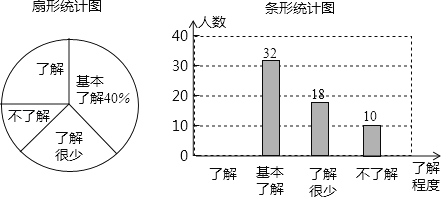
(1)在这次活动中抽查了多少名中学生?
(2)若该中学共有学生1600人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”程度的人数.
(3)若从对校园安全知识达到“了解程度的2个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com