
【题目】如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E. 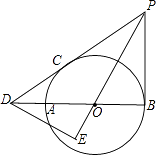
(1)求证:∠DPO=∠EDB;
(2)若PB=3,DB=4,求⊙O的半径.
【答案】
(1)证明:∵PC、PB是⊙O的切线,
∴∠DPO=∠OPB,
∵DE⊥PO,∴∠E=90°,
∵点B是切点,PB是切线
所以∠PBD=90°,
∴∠E=∠PBD,又∵∠POB=∠EOD
∴∠EDB=∠OPB
∴∠DPO=∠EDB
(2)解:连接OC,

∵PC、PB是⊙O的切线,切点为B、C,
∴PB=PC,∠PCO=90°.
在Rt△PBD中,∵PB=3,DB=4,∴PD=5,
∴DC=PD﹣PC=2
设⊙O半径为r,则OD=BD﹣r=4﹣r
在Rt△DCO中,r2+22=(4﹣r)2
∴r=1.5
即⊙O的半径为1.5.
【解析】(1)由切线长定理,知∠DPO=∠BPO,在△EOD和△BOP中,根据等角的余角相等,得∠BPO=∠EDB,从而问题得证.(2)在Rt△PBD中由勾股定理易得PD的长、由切线长定理知PB=PC,可计算出CD的长;若设圆的半径为r,OD=4﹣r,OC=r,在Rt△DCO中,根据勾股定理得到关于r的方程,求出⊙O的半径.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).


科目:初中数学 来源: 题型:
【题目】你能求(x-1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.
分别计算下列各式的值:
(1)(x﹣1)(x+1)=x2﹣1;
(2)(x﹣1)(x2+x+1)=x3﹣1;
(3)(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= _________ ;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+297+…+2+1;
(2)(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅不完整的统计图,请根据图中信息,解答下列问题: 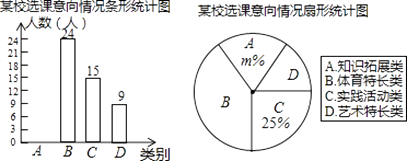
(1)求扇形统计图中m的值;
(2)补全条形统计图;
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,BE⊥CE,垂足是E,BE交AC于点D,F是BE上一点,AF⊥AE,且C是线段AF的垂直平分线上的点,AF=2![]() ,则DF=________.
,则DF=________.
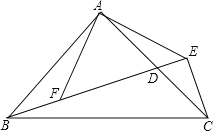
查看答案和解析>>
科目:初中数学 来源: 题型:
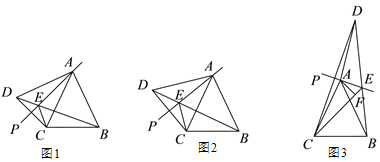
【题目】在△ABC 中,AB=AC,∠CAB=50°.在△ABC 的外侧作直线 AP,作 点 C 关于直线 AP 的对称点 D,连接 BD,CD,AD,其中 BD 交直线 AP 于点 E.
(1)如图 1,与 AD 相等的线段是_____;
(2)如图 2,若∠PAC=20°,求∠BDC 的度数;
(3)如图 3,当 65°<∠PAC<130°时,作 AF⊥CE 于点 F,若 EF=1,BE=5,求 DE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,已知线段AD平分∠BAC交BC于D,∠B=62°,∠C=58°.
(1)用尺规作出线段AD,并求∠ADB的度数;
(2)若DE⊥AC于点E,把图形补充完整并求∠ADE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 . 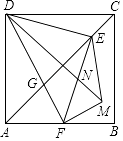
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com