
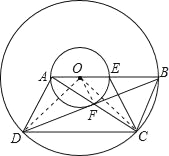
【题目】如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.

【答案】见解析
【解析】试题分析:由AE是小⊙O的直径,可得OA=OE,连接OF,根据切线的性质,可得OF⊥BD,然后由垂径定理,可证得DF=BF,易证得OF∥CE,根据平行线分线段成比例定理,可证得AF=CF,继而可得四边形ABCD是平行四边形,则可得AD=BC,AB=CD.然后连接OD、OC,可证得△AOD≌△EOC,则可得BC=AD=CE=AE.
试题解析:
图中相等的线段有:OA=OE,DF=BF,AF=CF,AB=CD,BC=AD=CE=AE.
证明如下:
∵AE是小⊙O的直径,
∴OA=OE.
连接OF,
∵BD与小⊙O相切于点F,
∴OF⊥BD.
∵BD是大圆O的弦,
∴DF=BF.
∵CE⊥BD,
∴CE∥OF,
∴AF=CF.
∴四边形ABCD是平行四边形.
∴AD=BC,AB=CD.
∵CE:AE=OF:AO,OF=AO,
∴AE=EC.
连接OD、OC,
∵OD=OC,
∴∠ODC=∠OCD.
∵∠AOD=∠ODC,∠EOC=∠OEC,
∴∠AOC=∠EOC,
∴△AOD≌△EOC,
∴AD=CE.
∴BC=AD=CE=AE.


科目:初中数学 来源: 题型:
【题目】(1)(操作发现):如图一,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC的数量关系是 .
(2)(类比探究):如图二,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.
(3)(应用):如图三,将(1)中的矩形ABCD改为正方形,边长AB=4,其它条件不变,求线段GC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中项点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式。请你观察下列儿种简单多面体模型,解答下列问题:

(1)根据上面多面体模型,完成表格中的空格:
多面体 | 项点数(V) | 面数(F) | 棱数(F) |
四面体 | |||
长方体 | |||
正八面体 | |||
正十二面体 |
你发现项点数(V)、面数(F)、棱数(F)之间存在的关系式是__________________________.
(2)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是 20;
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一直线上的三点A,B,C,若满足点C到另两个点A,B的距离之比是2,则称点C是其余两点的亮点(或暗点).具体地,当点C在线段AB上时,若![]() =2,则称点C是[A,B]的亮点;若
=2,则称点C是[A,B]的亮点;若![]() =2,则称点C是[B,A]的亮点;当C在线段AB的延长线上时,若
=2,则称点C是[B,A]的亮点;当C在线段AB的延长线上时,若![]() =2,称点C是[A,B]的暗点.例如,如图1,数轴上点A,B,C,D分别表示数﹣1,2,1,0.则点C是[A,B]的亮点,又是[A,D]的暗点;点D是[B,A]的亮点,又是[B,C]的暗点
=2,称点C是[A,B]的暗点.例如,如图1,数轴上点A,B,C,D分别表示数﹣1,2,1,0.则点C是[A,B]的亮点,又是[A,D]的暗点;点D是[B,A]的亮点,又是[B,C]的暗点

(1)如图2,M,N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.
[M,N]的亮点表示的数是 ,[N,M]的亮点表示的数是 ;
[M,N]的暗点表示的数是 ,[N,M]的暗点表示的数是 ;
(2)如图3,数轴上点A所表示的数为﹣20,点B所表示的数为40.一只电子蚂蚁P从B出发以2个单位每秒的速度向左运动,设运动时间为t秒.
①求当t为何值时,P是[B,A]的暗点;
②求当t为何值时,P,A和B三个点中恰有一个点为其余两点的亮点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)理数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=![]() .tanD=tan15°=
.tanD=tan15°=![]() =
= =
=![]() .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=![]() .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=![]() =
=![]() =
=![]() .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线![]() 与双曲线
与双曲线![]() 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
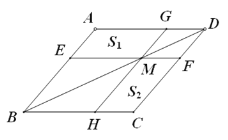
【题目】如图所示,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中平行四边形AEMG的面积![]() 与平行四边形HCFM的面积
与平行四边形HCFM的面积![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD.
(1)求证:AO=EO;
(2)若AE是△ABC的中线,则四边形AECD是什么特殊四边形?证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com