
【题目】当![]() 时,在数轴上数
时,在数轴上数![]() 和数
和数![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,若点
,若点![]() 表示的数分别为
表示的数分别为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]()

(1)在图中标出三点的位置
![]()
![]() ;
;![]() .
.
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点![]() 和
和![]() 点分别以每秒
点分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动.
个单位长度的速度向右运动.
试问:①![]() 秒后点
秒后点![]() 表示的数为 .
表示的数为 .
②![]() 的值是否随着运动时间
的值是否随着运动时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.
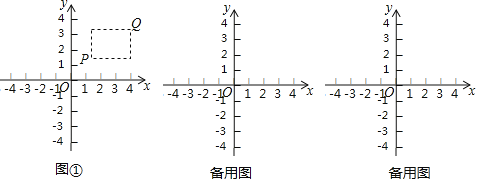
已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA=6,OC=2,一条动直线l分别与BC、OA将于点E、F,且将矩形OABC分为面积相等的两部分,则点O到动直线l的距离的最大值为_____.
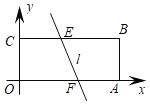
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①﹣|﹣2|和﹣(﹣2)互为相反数;②绝对值等于它本身的数是0、1;③若![]() =﹣1则a、b为相反数;④﹣210读作“﹣2的10次幂”⑤近似数9.7万精确到十分位;⑥若a是有理数,则它的相反数是﹣a,倒数是
=﹣1则a、b为相反数;④﹣210读作“﹣2的10次幂”⑤近似数9.7万精确到十分位;⑥若a是有理数,则它的相反数是﹣a,倒数是![]() ;下列说法正确的是( )
;下列说法正确的是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后, ![]() 能被x0+3整除,…,
能被x0+3整除,…, ![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于每个正整数 n,关于 x 的一元二次方程![]() 0 的两个根分别为 an、bn,设平面直角坐标系中,An、Bn 两点的坐标分别为 An(an,0),Bn(bn,0),AnBn 表示这两点间的距离,则 AnBn=____________(用含 n 的代数式表示);A1B1+ A2B2+ …+ A2011B2012 的值为______.
0 的两个根分别为 an、bn,设平面直角坐标系中,An、Bn 两点的坐标分别为 An(an,0),Bn(bn,0),AnBn 表示这两点间的距离,则 AnBn=____________(用含 n 的代数式表示);A1B1+ A2B2+ …+ A2011B2012 的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在结束了380课时初中阶段教学内容的教学后,刘老师计划在增加60课时用于总复习,将380课时按内容所占比例,绘制如下统计图表(图1和~图2),请根据图表提供的信息,回答下列问题:

(1)图1中“统计与概率”所在扇形的圆心角为度;
(2)图2中的a= ;
(3)在60课时的总复习中,刘老师应安排多少课时复习“数与代数”内容?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com