
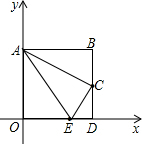
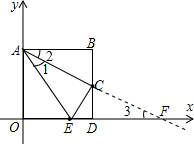
 (1997•山西)如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在直线为坐标轴建立直角坐标系,使D、A分别在x轴、y轴的正半轴上.
(1997•山西)如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在直线为坐标轴建立直角坐标系,使D、A分别在x轴、y轴的正半轴上.| AB |
| CD |
| BC |
| DE |
|
|
| 1 |
| 2 |
| AB |
| CD |
| BC |
| DE |
| 2 |
| 1 |
| 1 |
| DE |
| 1 |
| 2 |
| 3 |
| 2 |
|
|
| 4 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
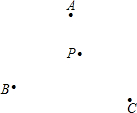 (1997•山西)如图,A、B、C三点表示某平原的三个村庄,要建一个电视转播站,使它到三个村庄的距离相等,求作电视转播站的位置P.(要求:尺规作图,只保留作图痕迹,不写作法)
(1997•山西)如图,A、B、C三点表示某平原的三个村庄,要建一个电视转播站,使它到三个村庄的距离相等,求作电视转播站的位置P.(要求:尺规作图,只保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:
 (1997•山西)如图,EC是⊙O的直径,且EC=2,作BC⊥AC于C,使BC=2,过B作⊙O的切线BA交CE的延长线于A,切点为D.
(1997•山西)如图,EC是⊙O的直径,且EC=2,作BC⊥AC于C,使BC=2,过B作⊙O的切线BA交CE的延长线于A,切点为D.查看答案和解析>>
科目:初中数学 来源: 题型:
 (1997•山西)如图,已知△ABC,⊙O1是它的外接圆,与⊙O1内切于A点的⊙O2交AB于F,交AC于G,FE⊥BC于E,GH⊥BC于H,AD是△ABC的高,交FG于M,且AD=6,BC=8.
(1997•山西)如图,已知△ABC,⊙O1是它的外接圆,与⊙O1内切于A点的⊙O2交AB于F,交AC于G,FE⊥BC于E,GH⊥BC于H,AD是△ABC的高,交FG于M,且AD=6,BC=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com