解:(1)设函数解析式为:y=ax
2+bx+c,
由函数经过点A(-4,0)、B(1,0)、C(-2,6),
可得
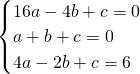
,
解得:
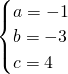
,
故经过A、B、C三点的抛物线解析式为:y=-x
2-3x+4;
(2)设直线BC的函数解析式为y=kx+b,
由题意得:
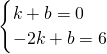
,
解得:

,
即直线BC的解析式为y=-2x+2.
故可得点E的坐标为(0,2),
从而可得:AE=

=2

,CE=
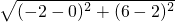
=2

,
故可得出AE=CE;
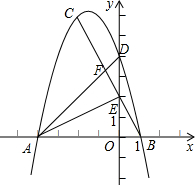
(3)相似.理由如下:
设直线AD的解析式为y=kx+b,
则
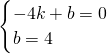
,
解得:
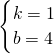
,
即直线AD的解析式为y=x+4.
联立直线AD与直线BC的函数解析式可得:
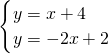
,
解得:
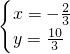
,
即点F的坐标为(-

,

),
则BF=
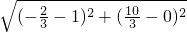
=
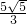
,
又∵AB=5,BC=
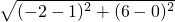
=3

,
∴

=

,

=

,
∴

=

,
又∵∠ABF=∠CBA,
∴△ABF∽△CBA.
故以A、B、F为顶点的三角形与△ABC相似.
分析:(1)利用待定系数发求解即可得出抛物线的解析式;
(2)求出直线BC的函数解析式,从而得出点E的坐标,然后分别求出AE及CE的长度即可证明出结论;
(3)求出AD的函数解析式,然后结合直线BC的解析式可得出点F的坐标,由题意得∠ABF=∠CBA,然后判断出

是否等于

即可作出判断.
点评:此题属于二次函数的综合题目,涉及了相似三角形的判定与性质、待定系数法求二次函数解析式,两点间的距离公式,解答本题要求我们仔细审题,将所学知识联系起来,综合解答.

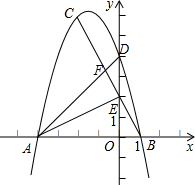 如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).
如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).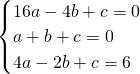 ,
,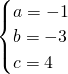 ,
,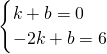 ,
, ,
, =2
=2 ,CE=
,CE=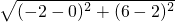 =2
=2 ,
, (3)相似.理由如下:
(3)相似.理由如下: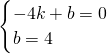 ,
,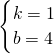 ,
,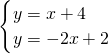 ,
,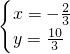 ,
, ,
, ),
),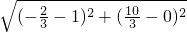 =
=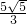 ,
,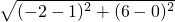 =3
=3 ,
, =
= ,
, =
= ,
, =
= ,
, 是否等于
是否等于 即可作出判断.
即可作出判断.

 发散思维新课堂系列答案
发散思维新课堂系列答案
 如图,已知△ABC的面积为4,且AB=AC,现将△ABC沿CA方向平移CA的长度,得到△EFA.
如图,已知△ABC的面积为4,且AB=AC,现将△ABC沿CA方向平移CA的长度,得到△EFA.
 (2010•孝感模拟)如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0).
(2010•孝感模拟)如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0). 如图,已知△ABC的三个顶点的坐标分别是A(-7,1),B(-3,3),C(-2,6).
如图,已知△ABC的三个顶点的坐标分别是A(-7,1),B(-3,3),C(-2,6).