
����Ŀ���������x��һԪ���η���ax2+bx+c��0��a��0��������ʵ������������һ����Ϊ��һ������2������������ķ���Ϊ���������̡������磬һԪ���η��̵���������2��4����x2��6x+8��0���ǡ��������̡���
��1����һԪ���η���x2��3x+c��0�ǡ��������̡�����c��ֵ��
��2������x��2����mx��n����0��m��0���ǡ��������̡��������ʽ4m2��5mn+n2��ֵ��
��3�����㣨p��q���ڷ���������y��![]() ��ͼ���ϣ���˵������x�ķ���px2+3x+q��0�ǡ��������̡���
��ͼ���ϣ���˵������x�ķ���px2+3x+q��0�ǡ��������̡���
��4��������x��һԪ���η���ax2+bx+c��0��a��0���ǡ��������̡�����˵��2b2��9ac��
���𰸡���1��c��ֵΪ2����2��0����3�������������4�����������
��������
��1���������һ��������ʾ��һ���������ݸ���ϵ���Ĺ�ϵ��������̵����������������c��ֵ��
��2��������һ����Ϊ2���ɡ��������̡��������֪��һ����Ϊ1��4������һ����Ϊ1ʱ���뷽�̿ɵ�m��n=0������һ����Ϊ4���뷽�̿ɵ�4m��n=0��������ʽ4m2��5mn+n2�ɷֽ�Ϊ��m��n����4m��n�������4m2��5mn+n2=��m��n����4m��n��=0��
��3���㣨p��q���ڷ���������y![]() ��ͼ���ϣ��ɵ�pq=2���ٸ��������ʽ������̵�������Ϊx1
��ͼ���ϣ��ɵ�pq=2���ٸ��������ʽ������̵�������Ϊx1![]() ��x2
��x2![]() �������ж��ǡ��������̡���
�������ж��ǡ��������̡���
��4���跽������Ϊx1��2x1�����ݸ���ϵ���Ĺ�ϵ�õ���x1+2x1=![]() ��x12x1=
��x12x1=![]() �������ɵý��ۣ�
�������ɵý��ۣ�
��1����һԪ���η���x2��3x+c=0��һ����Ϊx1������һ����Ϊ2x1��
�ɸ���ϵ���Ĺ�ϵ�ã�x1+2x1=3����x1=1����һ����Ϊ1������һ����Ϊ2����c=1��2=2��
��c��ֵΪ2��
��2�����̣�x��2����mx��n��=0��һ����Ϊ2������һ����Ϊ1��4��
����һ����Ϊ1ʱ����1����m��n��=0����m��n=0��
����һ����Ϊ4ʱ����2����4m��n��=0����4m��n=0����4m2��5mn+n2=��m��n����4m��n��=0��
�𣺴���ʽ4m2��5mn+n2��ֵΪ0��
��3���ߵ㣨p��q���ڷ���������y![]() ��ͼ���ϣ���pq=2��
��ͼ���ϣ���pq=2��
����x�ķ���px2+3x+q=0�ĸ�Ϊx![]() ��
��
����x1![]() ��x2
��x2![]() ����x1=2x2��
����x1=2x2��
����ǡ��������̡���
��4���跽������Ϊx1��2x1�����ݸ���ϵ���Ĺ�ϵ�õ���x1+2x1=![]() ��x12x1=
��x12x1=![]() ����x1=
����x1=![]() ��
��![]() ����
����![]() ����2b2=9ac��
����2b2=9ac��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC��90�㣬��D��BC�е㣬AE��BC��CE��AD��
��1����֤���ı���ADCE�����Σ�
��2������D��DF��CE�ڵ�F����B��60�㣬AB��6����EF�ij���
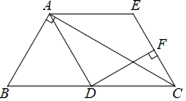
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90�㣬AC=BC=6����P�ڱ�AC���˶�������P��PD��AB�ڵ�D����AP��ADΪ�ڱ���PADE������PADE����ABC�ص�����ͼ�ε����Ϊy���߶�AP�ij�Ϊx��0��x��6����
��1�����߶�PE�ij����ú�x�Ĵ���ʽ��ʾ����
��2������E���ڱ�BC��ʱ����x��ֵ��
��3����y��x֮��ĺ�����ϵʽ��
��4��ֱ��д����E����ABC������������ֱ�߾������ʱx��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�ı߳�Ϊ3��E��F�ֱ���AB��BC���ϵĵ�,����EDF=45��.����DAE�Ƶ�D��ʱ����ת90�����õ���DCM.
��1����֤��EF=FM
��2����AE=1ʱ����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����AB=AC��BC����O�ڵ�D�� AC����O�ڵ�E����BAC=45�㡣
��1�����EBC�Ķ�����
��2����֤��BD=CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ABCD�У�E��CD����һ�㣬
��1������ADE�Ƶ�A��˳ʱ�뷽����ת��ʹAD��AB�غϣ��õ���ABF����ͼ1��ʾ���۲��֪����DE��ȵ��߶����� ������AFB=���� ��
��2����ͼ2��������ABCD�У�P��Q�ֱ���BC��CD���ϵĵ㣬�ҡ�PAQ=45������ͨ����ת�ķ�ʽ˵����DQ+BP=PQ��
��3���ڣ�2�����У�����BD�ֱ�AP��AQ��M��N���㻹������ת��˼��˵��BM2+DN2=MN2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ�зֱ���к���������������������У�����������ĸ�С�����ֲ�֮ͬ�⣬С��û���κ�����ÿ������ǰ�Ƚ�����ȣ�
��1����������ȡһ�������ϵĺ��ָպ����������ĸ���Ϊ���٣�
��2��������ȡһ���Żأ��ٴ�����ȡһ��������״ͼ���б��ķ�������ȡ�����������ϵĺ�����������������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
= y2+8y+16 ���ڶ�����
=��y+4��2 ����������
=��x2��4x+4��2 �����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ B��ƽ���ʽ C�������͵���ȫƽ����ʽ D�����������ȫƽ����ʽ
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________��������ס������ס���
�������ף���ֱ��д����ʽ�ֽ�������_________��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��O�ǵȱ�![]() ��һ�㣬
��һ�㣬![]() ����ACD=��BCO��OC=CD��
����ACD=��BCO��OC=CD��
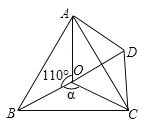
��1����˵����![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��2����![]() ʱ�����ж�
ʱ�����ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3����![]() Ϊ���ٶ�ʱ��
Ϊ���ٶ�ʱ��![]() �ǵ���������
�ǵ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com