
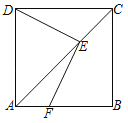
【题目】如图,正方形ABCD中,AB=3,点E为对角线AC上一点,EF⊥DE交AB于F,若四边形AFED的面积为4,则四边形AFED的周长为______.
【答案】4+2![]()
【解析】
连接BE,DF,过E作EN⊥BF于点N,证明△DCE≌△BCE和△BEF为等腰三角形,设AF=x,用x表示DE与EF,由根据四边形ADEF的面积为4,列出x的方程求得x,进而求得四边形ADEF的周长.
解:如图,连接BE,DF,过E作EN⊥BF于点N,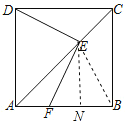
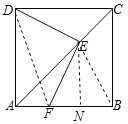
∵四边形ABCD为正方形,
∴CB=CD,∠BCE=∠DCE=45°,
在△BEC和△DEC中,
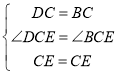 ,
,
∴△DCE≌△BCE(SAS),
∴DE=BE,∠CDE=∠CBE,
∴∠ADE=∠ABE,
∵∠DAB=90°,∠DEF=90°,
∴∠ADE+∠AFE=180°,
∵∠AFE+∠EFB=180°,
∴∠ADE=∠EFB,
∴∠ABE=∠EFB,
∴EF=BE,
∴DE=EF,
设AF=x,则BF=3-x,
∴FN=BN=![]() BF=
BF=![]() ,
,
∴AN=AF+FN=![]() ,
,
∵∠BAC=∠DAC=45°,∠ANF=90°,
∴EN=AN=![]() ,
,
∴DE=EF=![]() ,
,
∵四边形AFED的面积为4,
∴S△ADF+S△DEF=4,
∴![]() ×3x+
×3x+![]() ×
×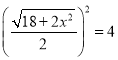 ,
,
解得,x=-7(舍去),或x=1,
∴AF=1,DE=EF=![]() ,
,
∴四边形AFED的周长为:3+1+![]() +
+![]() =4+
=4+![]() ,
,
故答案为:4+![]() .
.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】我国古代数学著作(九章算术)中有如下问题:“今有人持金出五关,前关二而税一.次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤.”其意思为“今有人持金出五关,第![]() 关所收税金为持金的
关所收税金为持金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,
,![]() 关所收税金之和,恰好重
关所收税金之和,恰好重![]() 斤.”若设这个人原本持金
斤.”若设这个人原本持金![]() 斤,根据题意可列方程为__________ .
斤,根据题意可列方程为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E是直线AB上的点,过点E的直线l交直线CD于点F,EG平分∠BEF交CD于点G.在直线l绕点E旋转的过程中,图中∠1,∠2的度数可以分别是( )
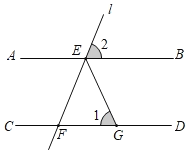
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
查看答案和解析>>
科目:初中数学 来源: 题型:
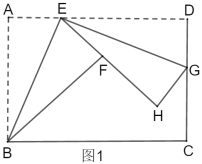
【题目】如图1,折叠矩形![]() ,具体操作:①点
,具体操作:①点![]() 为
为![]() 边上一点(不与
边上一点(不与![]() 、
、![]() 重合),把
重合),把![]() 沿
沿![]() 所在的直线折叠,
所在的直线折叠,![]() 点的对称点为
点的对称点为![]() 点;②过点
点;②过点![]() 对折
对折![]() ,折痕
,折痕![]() 所在的直线交
所在的直线交![]() 于点
于点![]() 、
、![]() 点的对称点为
点的对称点为![]() 点.
点.
(1)求证:![]() ∽
∽![]() .
.
(2)若![]() ,
,![]() .
.
①点![]() 在移动的过程中,求
在移动的过程中,求![]() 的最大值.
的最大值.
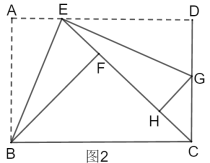
②如图2,若点![]() 恰在直线
恰在直线![]() 上,连接
上,连接![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)求点B的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线的对称轴;
(3)已知点![]() ,
,![]() .若抛物线与线段PQ恰有一个公共点,结合函数图象,求
.若抛物线与线段PQ恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移![]() 格,再纵向平移
格,再纵向平移![]() 格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么
格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么![]() 的结果( )
的结果( )

A.只有一个确定的值B.有两个不同的值
C.有三个不同的值D.有三个以上不同的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
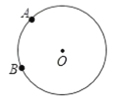
(1)如图,已知![]() 、
、![]() 是
是![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
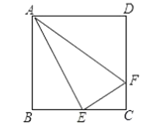
(2)如图,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
运用:
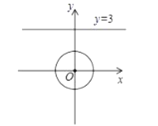
(3)如图,在平面直角坐标系![]() 中,
中,![]() 的半径为1,点
的半径为1,点![]() 是直线
是直线![]() 上的一点,若在
上的一点,若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,当其面积取得最小值时,直接写出此时点
为“智慧三角形”,当其面积取得最小值时,直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮一起玩摸棋子的游戏.在一个密闭不透明的盒子中装有2枚白色棋子和2枚黑色棋子,棋子除颜色外其余均相同.从这个盒子中随机摸出1枚棋子记下颜色,放回;摇匀后,再随机地摸出1枚棋子,并记下颜色,若两次摸出的棋子颜色相同,则小明胜;若两次摸出的棋子颜色不相同,则小亮胜.这个游戏对双方公平吗?请用画树状图或列表格的方法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com