解:(1)由方程组得-(m+1)x
2-6x+8=0有两个实数解.
∴△=36+32(m+1)≥0.
∴m≥-

且m≠-1;
(2)y=-(m+1)x
2+(m-5)x+6,C(0,6).
设A(x
1,0),B(x
2,0),则有

×|x
1-x
2|×6=12,|x
1-x
2|=4.
∴(x
1+x
2)
2-4x
1x
2=16,(
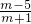
)
2+
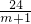
=16;
整理得5m
2+6m-11=0.
解得m
1=1,m
2=-
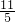
(舍).
表达式为y=-2x
2-4x+6,y=2x-2;
(3)能平移,y=-2x
2-4x+6=-2(x+1)
2+8.
一种平移方法:向下平移8个单位,再向右平移2个单位,得到抛物线y=-2(x-1)
2.
分析:(1)可将方程组中的两个函数式联立成一个一元二次方程,根据方程组有两个实数解,那么方程的△>0,由此可得出m的取值范围.
(2)根据抛物线的解析式可知C点的坐标为(0,6),因此可根据△ABC的面积求得AB的距离应该是12,然后设出A,B的坐标,根据一元二次方程根与系数的关系即可求出m的值.也就能确定出抛物线和直线的解析式.
(3)可以平移.根据二次函数的性质,先向下平移8个单位,再向右平移2个单位可得.本题方法不唯一,正确就行.
点评:本题主要考查了一元二次方程根与系数的关系、根的判别式以及二次函数与一元二次方程的关系等知识点.

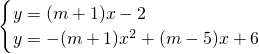 有两个实数解.求m的取值范围;
有两个实数解.求m的取值范围; 且m≠-1;
且m≠-1; ×|x1-x2|×6=12,|x1-x2|=4.
×|x1-x2|×6=12,|x1-x2|=4.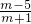 )2+
)2+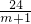 =16;
=16;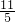 (舍).
(舍).

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案