
【题目】如图,点![]() 是线段
是线段![]() 的中点,过点
的中点,过点![]() 的射线
的射线![]() 与
与![]() 成
成![]() 的角,点
的角,点![]() 为射线
为射线![]() 上一动点,给出以下四个结论:
上一动点,给出以下四个结论:
①当![]() ,垂足为
,垂足为![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
③在射线![]() 上,使
上,使![]() 为直角三角形的点
为直角三角形的点![]() 只有1个;
只有1个;
④在射线![]() 上,使
上,使![]() 为等腰三角形的点
为等腰三角形的点![]() 只有1个;
只有1个;
其中正确结论的序号是___.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(2015镇江)
活动1:在一只不透明的口袋中装有标号为1,2,3的3个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三位同学丙→甲→乙的顺序依次从袋中各摸出一个球(不放回),摸到1号球胜出,计算甲胜出的概率.(注:丙→甲→乙表示丙第一个摸球,甲第二个摸球,乙最后一个摸球)
活动2:在一只不透明的口袋中装有标号为1,2,3,4的4个小球,这些球除标号外都相同,充分搅匀,请你对甲、乙、丙三名同学规定一个摸球顺序: → → ,他们按这个顺序从袋中各摸出一个球(不放回),摸到1号球胜出,则第一个摸球的同学胜出的概率等于 ,最后一个摸球的同学胜出的概率等于 .
猜想:在一只不透明的口袋中装有标号为1,2,3,…,n(n为正整数)的n个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三名同学从袋中各摸出一个球(不放回),摸到1号球胜出,猜想:这三名同学每人胜出的概率之间的大小关系.
你还能得到什么活动经验?(写出一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列表格的对应值:
x | 3.23 | 3.24 | 3.25 | 3.26 |
| -0.06 | -0.02 | 0.03 | 0.09 |
写出方程![]() (a≠0,a,b,c为常数)一个解x的范围是__.
(a≠0,a,b,c为常数)一个解x的范围是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段圆弧与长度为![]() 的正方形网格的交点是A、B、C.
的正方形网格的交点是A、B、C.
(1)请完成以下操作:
①以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;

(2)请在(1)的基础上,完成下列填空:
①⊙D的半径![]() (结果保留根号).
(结果保留根号).
②点(-2,0)在⊙D ;(填“上”、“内”、“外”)
③∠ADC的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4ni=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.
计算:(1)i.i2.i3.i4
(2)i+i2+i3+i4+…+i2017+i2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
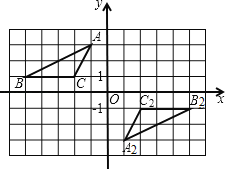
【题目】如图,在平面直角坐标系中,A(﹣1,3)、B(﹣5,1)、C(﹣2,1).
(1)△ABC的面积为______.
(2)在图中作出△ABC关于x轴的对称图形△A1B1C1,并写出点A1的坐标.
(3)请说明△A2B2C2是由△A1B1C1经过怎样的变换得到的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市“健益”超市购进一批![]() 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以![]() 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出![]() 千克.由销售经验知,每天销售量
千克.由销售经验知,每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)
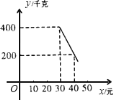
(元)![]() 存在如下图所示的一次函数关系.
存在如下图所示的一次函数关系.
![]() 试求出
试求出![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 设“健益”超市销售该绿色食品每天获得利润为
设“健益”超市销售该绿色食品每天获得利润为![]() 元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
![]() 根据市场调查,该绿色食品每天可获利润不超过
根据市场调查,该绿色食品每天可获利润不超过![]() 元,现该超市经理要求每天利润不得低于
元,现该超市经理要求每天利润不得低于![]() 元,请你帮助该超市确定绿色食品销售单价
元,请你帮助该超市确定绿色食品销售单价![]() 的范围(直接写出).
的范围(直接写出).
查看答案和解析>>
科目:初中数学 来源: 题型:
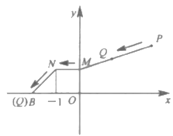
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,先移动到
点出发,先移动到![]() 轴上的点
轴上的点![]() 处,再沿垂直于
处,再沿垂直于![]() 轴的方向向左移动1个单位至点
轴的方向向左移动1个单位至点![]() 处,最后移动到点
处,最后移动到点![]() 处停止.当点
处停止.当点![]() 移动的路径最短时 (即三条线段
移动的路径最短时 (即三条线段![]() 、
、![]() 、
、![]() 长度之和最小),点
长度之和最小),点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com