
【题目】已知抛物线![]() 经过点
经过点![]() ,且抛物线上任意不同两点
,且抛物线上任意不同两点![]() 都满足:当
都满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;抛物线与
;抛物线与![]() 轴另一个交点为
轴另一个交点为![]() ,与
,与![]() 轴交于
轴交于![]() 点,对称轴与
点,对称轴与![]() 轴交于
轴交于![]() 点.
点.
(1)求抛物线的对称轴及点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 轴的平行线交抛物线的对称轴于点
轴的平行线交抛物线的对称轴于点![]() ,当四边形
,当四边形![]() 是正方形时,求抛物线的解析式;
是正方形时,求抛物线的解析式;
(3)在(2)的条件下,垂直于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() 和
和![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)对称轴为直线![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据当抛物线上的点横坐标小于-2时,纵坐标随横坐标增大而减小,当横坐标大于-2时,纵坐标随横坐标增大而增大,可求得抛物线的对称轴和A点坐标;
(2)由四边形OCME是正方形得点C 坐标,设抛物线的解析式为![]() ,代入求出a的值即可得出抛物线解析式;
,代入求出a的值即可得出抛物线解析式;
(3)根据题意结合图象得出![]() ,再计算出
,再计算出![]() ,即可得出结论.
,即可得出结论.
(1)由题意知,当抛物线上的点横坐标小于-2时,纵坐标随横坐标增大而减小,当横坐标大于-2时,纵坐标随横坐标增大而增大,
∴对称轴为直线![]()
![]() ;
;
(2)根据题意,画出草图如解图,设抛物线的解析式为![]() ,
,
∵四边形OCME是正方形,
![]() ,
,
将C点坐标代入抛物线解析式,解得![]() ,
,
![]()
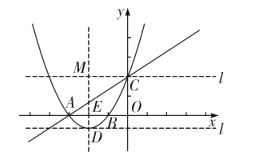
(3)![]() .
.
结合图象可知,要满足![]() ,则
,则![]() .
.
由题意得,点P与点Q关于直线![]() 对称,
对称,
![]() .
.
![]() ,
,
∴N点处于线段AC上且不包含点A和点C,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0).P为该抛物线上一动点,设点P的横坐标为m.
x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0).P为该抛物线上一动点,设点P的横坐标为m.
(1)求抛物线的解析式.
(2)将该抛物线沿y轴向下平移![]() AB个单位长度,点P的对应点为P′,若OP=OP′,求△OP P′的面积.
AB个单位长度,点P的对应点为P′,若OP=OP′,求△OP P′的面积.
(3)如图2,连接AP,BP,设△APB的面积为S,当-2≤m≤2时,直接写出S的最大值.
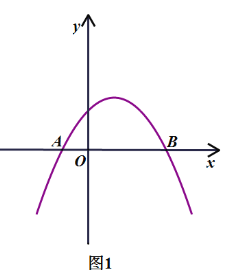
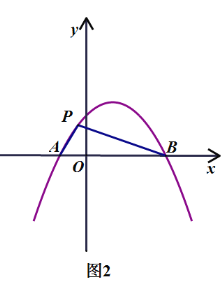
查看答案和解析>>
科目:初中数学 来源: 题型:
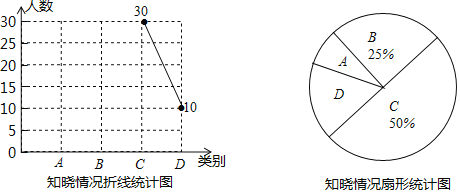
【题目】2018年5月13日,大国重器﹣﹣中国第一艘国产航母正式海试,某校团支部为了了解同学们对此事的知晓情况,随机抽取了部分同学进行调查,并根据收集到的信息绘制了如下两幅不完整的统计图,图中A表示“知道得很详细”,B表示“知道个大概”,C表示“听说了”,D表示“完全不知道”,请根据途中提供的信息完成下列问题:
(1)扇形统计图中A对应的圆心角是 度,并补全折线统计图.
(2)被抽取的同学中有4位同学都是班级的信息员,其中有一位信息员属于D类,校团支部从这4位信息员中随机选出两位作为校广播站某访谈节目的嘉宾,请用列表法或画树状图法,求出属于D类的信息员被选为的嘉宾的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.

(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=![]() (x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.
(x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
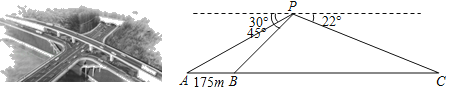
【题目】横卧于清波之上的黄石大桥与已经贯通的五峰山隧道将成为恩施城区跨越东西方向的最大直线通道,它把六角亭老城区与知名景点女儿城连为一体,缓解了恩施城区交通拥堵的现状.如图,某数学兴趣小组利用无人机在五峰山隧道正上空点P处测得黄石大桥西端点A的俯角为30°,东端点B(隧道西进口)的俯角为45°,隧道东出口C的俯角为22°,已知黄石大桥AB全长175米,隧道BC的长约多少米(计算结果精确到1米)?(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y = ![]() ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
ax2 ax + c图象的顶点为C,一次函数y = x + 3的图象与这个二次函数的图象交于A、B两点(其中点A在点B的左侧),与它的对称轴交于点D.
(1)求点D的坐标;
(2) ①若点C与点D关于x轴对称,且△BCD的面积等于4,求此二次函数的关系式;
②若CD=DB,且△BCD的面积等于4![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com