
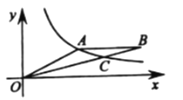
【题目】如图,![]() 是反比例函数
是反比例函数![]() 在第一象限图像上一点,连接
在第一象限图像上一点,连接![]() ,过
,过![]() 作
作![]() 轴,截取
轴,截取![]() (
(![]() 在
在![]() 右侧),连接
右侧),连接![]() ,交反比例函数
,交反比例函数![]() 的图像于点
的图像于点![]() .
.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求点![]() 的坐标及
的坐标及![]() 所在直线解析式;
所在直线解析式;
(3)求![]() 的面积.
的面积.
【答案】(1)y=![]() ;(2)B(18,6),y=
;(2)B(18,6),y=![]() x;(3)20.
x;(3)20.
【解析】
(1)直接代入A点坐标即可求出k的值,进而可得函数解析式;
(2)过点A作AD⊥x轴于点D,利用勾股定理计算出AO的长,进而可得AB长,然后可得B点坐标.设OB所在直线解析式为y=mx(m≠0)利用待定系数法可求出BO的解析式;
(3)首先联立两个函数解析式,求出C点坐标,过点C作CE⊥x轴,延长EC交AB于点F,连接AC,再确定F点坐标,最后求面积即可.
解:(1)将点A(8,6)代入![]() (k≠0),
(k≠0),
得:k=48,
则反比例函数解析式为y=![]() ;
;
(2)如图,过点A作AD⊥x轴于点D,
则OD=8、AD=6,
∴OA=![]() =10,
=10,
∵AB∥x轴,且AB=OA=10,
∴点B的坐标为(18,6);
设OB所在直线解析式为y=mx(m≠0),
将点B(18,6)代入得m=![]() ,
,
∴OB所在直线解析式为y=![]() x;
x;
(3)联立解析式: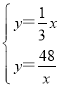
解得:![]() ,
,
可得点C坐标为(12,4),
过点C作CE⊥x轴,延长EC交AB于点F,连接AC,
则点F坐标为(12,6),
∴AF=4,CF=2,CE=4,
则△OAC的面积=![]() ×(4+12)×6-
×(4+12)×6-![]() ×12×4-
×12×4-![]() ×4×2=20.
×4×2=20.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中
中![]() ,点
,点![]() 从点
从点![]() 运动到点
运动到点![]() 停止,连接
停止,连接![]() ,以
,以![]() 长为直径作
长为直径作![]() .
.
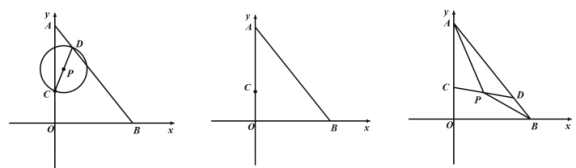
(1)若![]() ,求
,求![]() 的半径;
的半径;
(2)当![]() 与
与![]() 相切时,求
相切时,求![]() 的面积;
的面积;
(3)连接![]() ,在整个运动过程中,
,在整个运动过程中,![]() 的面积是否为定值,如果是,请直接写出面积的定值,如果不是,请说明理由.
的面积是否为定值,如果是,请直接写出面积的定值,如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于_________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,![]() .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
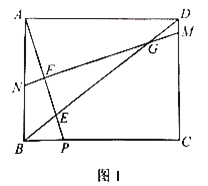
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() .
.
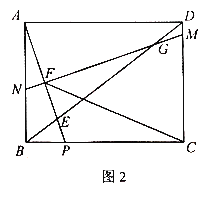
(3)如图2,在(2)的条件下,连接CF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
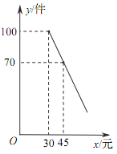
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,反比例函数
,反比例函数![]() (a,b,k是常数,且
(a,b,k是常数,且![]() ),若其中一部分x,y的对应值如表:则不等式
),若其中一部分x,y的对应值如表:则不等式![]() 的解集是_________.
的解集是_________.
x |
|
|
|
| 1 | 2 | 3 | 4 |
| 3 | 2 | 1 | 0 |
|
|
|
|
|
| 2 | 3 | 6 |
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经中共中央决定设立河北雄安新区,这一重大措施必将带动首都及周边区域向更高水平发展,同时也会带来更多商机.某水果经销商在第一周购进一批水果1160件,预计在第二周进行试销,购进价格为每件10元,若售价为每件12元,则可全部售出;若售价每涨价0.1元,销量就减少2件.
(1)若该经销商在第二周的销量不低于1100件,则售价应不高于多少元?
(2)由于销量较好,第三周水果进价比第一周每件增加了20%,该经销商增加了进货量,并加强了宣传力度,结果第三周的销量比第二周在(1)条件下的最低销量增加了m%,但售价比第二周在(1)条件下的最高售价减少了![]() m%,结果第三周利润达到3388元,求m的值(m>10).
m%,结果第三周利润达到3388元,求m的值(m>10).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com