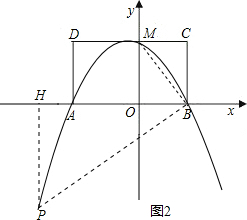
解:(1)∵MO=MD=4,MC=3,
∴M、A、B的坐标分别为(0,4),(-4,0),(3,0)
设BM的解析式为y=kx+b;
则
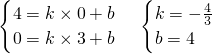
,
∴BM的解析式为y=-

x+4.
(2)方法一:
设抛物线的解析式为y=ax
2+bx+c
则
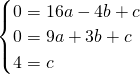
,
解得a=b=-

,c=4
∴y=-

x
2-

x+4
方法二:
设抛物线的解析式为y=a(x+4)(x-3)
将M(0,4)的坐标代入得a=-

∴y=-

(x+4)(x-3)=-

x
2-

x+4
(3)设抛物线上存在点P,使△PMB构成直角三角形.
①过M作MB的垂线与抛物线交于P,过P作PH⊥DC交于H,
∴∠PMB=90°,
∴∠PMH=∠MBC,
∴△MPH∽△BMC,
∴PH:HM=CM:CB=3:4
设HM=4a(a>0),则PH=3a
∴P点的坐标为(-4a,4-3a)
将P点的坐标代入y=-

x
2-

x+4得:
4-3a=-

(-4a)
2-

×(-4a)+4
解得a=0(舍出),
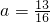
,
∴P点的坐标为(
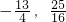
)
②或者,抛物线上存在点P,使△PMB构成直角三角形.
过M作MB的垂线与抛物线交于P,设P的坐标为(x
0,y
0),
由∠PMB=90°,∠PMD=∠MBC,
过P作PH⊥DC交于H,则MH=-x
0,PH=4-y
0∴由tan∠PMD=tan∠MBC
得
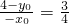
,
∴
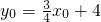
∴

,x
0=0(舍出)
∴
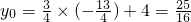
,
∴P点的坐标为(
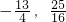
)
类似的,如果过B作BM的垂线与抛物线交于点P,
设P的坐标为(x
0,y
0),
同样可求得
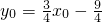
,
由
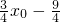
=
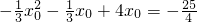
,x
0=3(舍出)
这时P的坐标为(
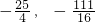
).
分析:(1)(2)根据MO=MD=4,MC=3就可以求出A、M、B三点的作坐标,根据待定系数法就可以求出直线BM的解析式与抛物线的解析式.
(3)过M、B作MB的垂线,它与抛物线的交点即为P点,因而符合条件的P点是存在的.当∠PMB=90°时,过P作PH⊥DC交于H,则
易证△MPH∽△BMC,得到PH:HM=CM:CB=3:4,因而可以设HM=4a(a>0),则PH=3a,则P点的坐标为(-4a,4-3a).
将P点的坐标代入y=-

x
2-

x+4就可以求出a的值,进而求出P点的坐标.
点评:本题主要考查了待定系数法求函数解析式.是函数与相似三角形相结合的综合题.

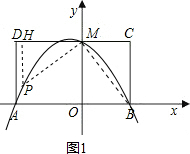
 如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3.
如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3.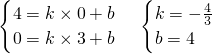 ,
, x+4.
x+4.
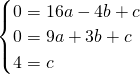 ,
, ,c=4
,c=4 x2-
x2- x+4
x+4
 (x+4)(x-3)=-
(x+4)(x-3)=- x2-
x2- x+4
x+4 x2-
x2- x+4得:
x+4得: (-4a)2-
(-4a)2- ×(-4a)+4
×(-4a)+4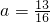 ,
,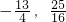 )
)
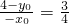 ,
,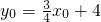
 ,x0=0(舍出)
,x0=0(舍出)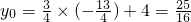 ,
,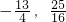 )
)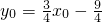 ,
,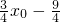 =
=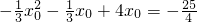 ,x0=3(舍出)
,x0=3(舍出)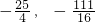 ).
). x2-
x2- x+4就可以求出a的值,进而求出P点的坐标.
x+4就可以求出a的值,进而求出P点的坐标.


 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且
