
����Ŀ������ʦ��![]() ����������ɸ��������һ�������Ŀڴ������ȣ�������ѧ����������ʵ�飬ÿ������һ�����зŻأ����±��ǻ�����е�һ��ͳ�����ݣ�
����������ɸ��������һ�������Ŀڴ������ȣ�������ѧ����������ʵ�飬ÿ������һ�����зŻأ����±��ǻ�����е�һ��ͳ�����ݣ�
����Ĵ��� |
|
|
|
|
|
|
��������Ĵ��� |
|
|
|
|
|
|
���������Ƶ�� |
|
|
|
|
|
![]() ��ȫ�ϱ��е��й����ݣ������ϱ����ݹ��ƴӴ�������һ�����Ǻ���ĸ�����________����ȷ��0.01����
��ȫ�ϱ��е��й����ݣ������ϱ����ݹ��ƴӴ�������һ�����Ǻ���ĸ�����________����ȷ��0.01����
![]() ������а���ĸ�����
������а���ĸ�����
![]() ��
��![]() �������£���Сǿͬѧ�зŻص��������������û���״ͼ���б��ķ������������ζ���������ĸ��ʣ�
�������£���Сǿͬѧ�зŻص��������������û���״ͼ���б��ķ������������ζ���������ĸ��ʣ�
���𰸡���1��0.25����2�����������3������3�����ζ���������ĸ���Ϊ![]() .
.
��������
��1���ô����ظ��������¼�������Ƶ���ȶ���ij����������ʾ���¼������ĸ��ʼ��ɣ�
��2�����ø��ʹ�ʽ�г�������⼴�ɣ�
��3���б������еȿ��ܵĽ���оٳ�����Ȼ�����ø��ʹ�ʽ��⼴��.
��1��249��1000��0.25����ȷ��0.01����
�ߴ����ظ������¼�������Ƶ�����ȶ���0.25������
����ƴӴ�������һ�����Ǻ���ĸ�����0.25��
�ʴ���0.25��
��2������а���Ϊx����
![]() ��0.25��
��0.25��
���x��3.
�𣺹��ƴ�����3������.
��3����B����һ������W1��W2��W3����������������б����£�
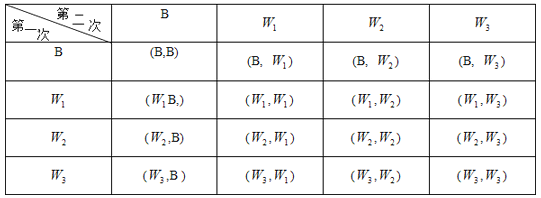
�ܹ���16�ֵȿ��ܵĽ���������������ǰ���Ľ����9��.
���������������ǰ���ĸ���Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
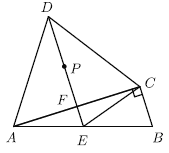
����Ŀ����ͼ��![]() �У�
��![]() ����
����![]() Ϊ�ױ�������������
Ϊ�ױ�������������![]() ��
��![]() ������
������![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() ��
��
��1����֤��![]() ��
��
��2����![]() ��
��![]() ����
����![]() ������
������![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() Ϊ�δ�ʱ��
Ϊ�δ�ʱ��![]() ���ܳ���С���������ʱ
���ܳ���С���������ʱ![]() ���ܳ���
���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
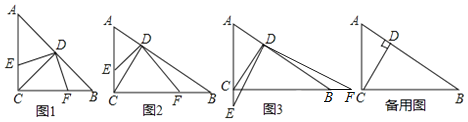
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() �ڵ�D����E��ֱ��AC��һ���㣬����DE������D��
�ڵ�D����E��ֱ��AC��һ���㣬����DE������D��![]() ����ֱ��BC�ڵ�F��
����ֱ��BC�ڵ�F��
![]() ̽�����֣�
̽�����֣�
��ͼ1����![]() ����E���߶�AC�ϣ���
����E���߶�AC�ϣ���![]() ______��
______��
![]() ��ѧ˼����
��ѧ˼����
![]() ��ͼ2������E���߶�AC�ϣ���
��ͼ2������E���߶�AC�ϣ���![]() ______
______![]() �ú�m��n�Ĵ���ʽ��ʾ
�ú�m��n�Ĵ���ʽ��ʾ![]() ��
��
![]() ����E��ֱ��AC���˶�ʱ��
����E��ֱ��AC���˶�ʱ��![]() �еĽ����Ƿ���Ȼ�����������ͼ3�����θ���֤����
�еĽ����Ƿ���Ȼ�����������ͼ3�����θ���֤����
![]() ��չӦ�ã���
��չӦ�ã���![]() ��
��![]() ��
��![]() ����ֱ��д��CE�ij���
����ֱ��д��CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��F�ֱ�������ABCD�ı�AB��AD���е㣬��AB��5��AC��6.

��1����Խ���BD�ij���
��2����֤���ı���AEOFΪ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A�ڵ�һ���ޣ���A��x�ύ��B��2��0����C��8��0�����㣬��y�������ڵ�D�����A�������ǣ�������
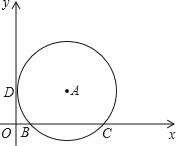
A. ��5��4�� B. ��4��5�� C. ��5��3�� D. ��3��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���߲�ÿǧ���ۼ�![]() ��Ԫ���������·�
��Ԫ���������·�![]() ֮��Ĺ�ϵ��ͼ1��ʾ��ÿǧ�˳ɱ�
֮��Ĺ�ϵ��ͼ1��ʾ��ÿǧ�˳ɱ�![]() ��Ԫ���������·�
��Ԫ���������·�![]() ֮��Ĺ�ϵ��ͼ2��ʾ������ͼ1�еĵ���ͬһ���߶��ϣ�ͼ2�еĵ���ͬһ���������ϣ��������ߵ���͵������Ϊ��6��1����
֮��Ĺ�ϵ��ͼ2��ʾ������ͼ1�еĵ���ͬһ���߶��ϣ�ͼ2�еĵ���ͬһ���������ϣ��������ߵ���͵������Ϊ��6��1����
��1�����![]() ��
��![]() ֮������ĺ�������ʽ����ֱ��д��
֮������ĺ�������ʽ����ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�����![]() ��
��![]() ֮������ĺ�������ʽ��
֮������ĺ�������ʽ��
��3���������߲�ÿǧ������Ϊ![]() Ԫ���������ĸ��·ݳ��������߲ˣ�
Ԫ���������ĸ��·ݳ��������߲ˣ�![]() ��ȡ�����ֵ������������ֵ��������=�ۼ�-�ɱ���
��ȡ�����ֵ������������ֵ��������=�ۼ�-�ɱ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
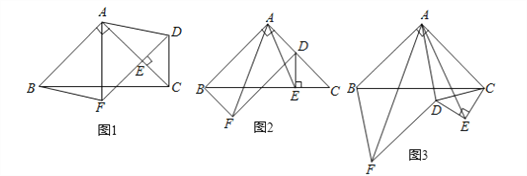
����Ŀ����ͼ1���ڵ���Rt��ABC������BAC=90������E��AC�ϣ��Ҳ����A��C�غ���������ABC���ⲿ������Rt��CED��ʹ��CED=90��������AD���ֱ���AB��ADΪ�ڱ���ƽ���ı���ABFD������AF��
��1����֤����AEF�ǵ���ֱ����������
��2����ͼ2������CED�Ƶ�C��ʱ����ת������E���߶�BC��ʱ������AE����֤��AF=![]() AE��
AE��
��3����ͼ3������CED�Ƶ�C������ʱ����ת����ƽ���ı���ABFDΪ����������CED����ABC���·�ʱ����AB=2![]() ��CE=2�����߶�AE�ij���
��CE=2�����߶�AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
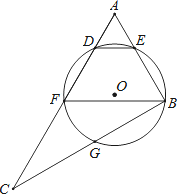
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣬��FΪAC�е㣬��O������B��F������AC���ڵ�D����AB���ڵ�E����BC���ڵ�G������BF��DE����EFG�ij���Ϊ��1+![]() ���У�
����
��1�����O�İ뾶��
��2����DE��BF����AE=a��DF=2+![]() ��a�����ж�Բ��O��ֱ��BF��λ�ù�ϵ����˵�����ɣ�
��a�����ж�Բ��O��ֱ��BF��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
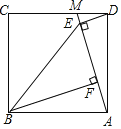
����Ŀ����ͼ����M��������ABCD��CD��һ�㣬����AM����DE��AM�ڵ�E��BF��AM�ڵ�F������BE��
��1����֤��AE��BF��
��2����֪AF��2���ı���ABED�����Ϊ24����EF��BF��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com