
【题目】如图,在直角坐标系中,正方形ABCD绕点A(0,6)旋转,当点B落在x轴上时,点C刚好落在反比例函数![]() (k≠0,x>0)的图像上.已知sin∠OAB=
(k≠0,x>0)的图像上.已知sin∠OAB=![]() .
.
(1)求反比例函数的表达式;
(2)反比例函数![]() 的图像是否经过AD边的中点,并说明理由.
的图像是否经过AD边的中点,并说明理由.
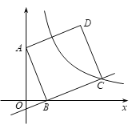
【答案】(1)![]() ;(2) 不经过AD边的中点,理由见解析;
;(2) 不经过AD边的中点,理由见解析;
【解析】
(1)过C点作CE⊥x轴于E,如图,利用正弦的定义得到sin∠OAB=![]() ,设OB=
,设OB=![]() ,则AB=5
,则AB=5![]() ,利用勾股定理即可求得
,利用勾股定理即可求得![]() ,接着证明△AOB≌△BEC得到AO=BE,OB=CE,从而得到C的坐标,然后利用待定系数法求反比例函数解析式;
,接着证明△AOB≌△BEC得到AO=BE,OB=CE,从而得到C的坐标,然后利用待定系数法求反比例函数解析式;
(2)利用平移的方法确定D点坐标,再利用线段中点坐标公式得到线段AD的中点坐标,然后根据反比例函数图象上点的坐标特征判断反比例函数![]() 的图象是否经过AD边的中点.
的图象是否经过AD边的中点.
(1)过C点作CE⊥x轴于E,如图,
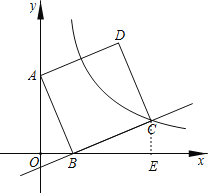
∵A(0,6),
∴OA=6,
在Rt△OAB中,sin∠OAB=![]() ,
,
设OB=![]() ,则AB=5
,则AB=5![]() ,
,
∴OA=![]() ,
,
∴![]() ,
,
解得:![]() ,即OB=
,即OB=![]() ,
,
∴点B的坐标为(3,0),
∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∴∠ABO+∠CBE=90°,
而∠ABO+∠OAB=90°,
∴∠OAB=∠CBE,
∵∠AOB=∠BEC,∠OAB=∠CBE=90°,AB=BC,
∴△AOB≌△BEC(AAS),
∴AO=BE=6,OB=CE=3,
∴点C的坐标为(9,3),
∵点C在反比例函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴反比例函数的表达式为![]() ;
;
(2)反比例函数![]() 的图象不经过AD边的中点.
的图象不经过AD边的中点.
理由如下:
∵点B向左平移3个单位,再向上平移6个单位得到A点,
∴点C向左平移3个单位,再向上平移6个单位得到D点,
∴D点坐标为(6,9),
∴线段AD的中点坐标为(![]() ,
,![]() ),即(3,3.5),
),即(3,3.5),
∵当x=3时,![]() ,
,
∴反比例函数图像不经过AD边的中点.


科目:初中数学 来源: 题型:
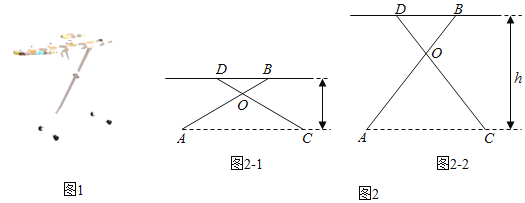
【题目】有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到lcm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成圆形阴影.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为( )
A.0.36πm2B.0.81πm2C.1.44πm2D.3.24πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
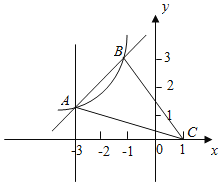
【题目】如图,在平面立角坐标系中,反比例函数y=![]() (k≠0,x<0)与一次函数y=ax+b的图象交于点A(﹣3,1)、B(m,3).点C的坐标为(1,0),连接AC,BC.
(k≠0,x<0)与一次函数y=ax+b的图象交于点A(﹣3,1)、B(m,3).点C的坐标为(1,0),连接AC,BC.
(1)求反比例函数和一次函数的表达式;
(2)当x<0时,直接写出不等式![]() ≥ax+b的解集 ;
≥ax+b的解集 ;
(3)若点M为y轴的正半轴上的动点,当△ACM是直角三角形时,直接写出点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴正半轴上,以
轴正半轴上,以![]() 为一边作等腰直角
为一边作等腰直角![]() ,使得点
,使得点![]() 在第一象限.
在第一象限.

(1)求出所有符合题意的点![]() 的坐标;
的坐标;
(2)在![]() 内部存在一点
内部存在一点![]() ,使得
,使得![]() 之和最小,请求出这个和的最小值.
之和最小,请求出这个和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点![]() 的横、纵坐标的绝对值之和叫做点
的横、纵坐标的绝对值之和叫做点![]() 的勾股值,记
的勾股值,记![]()
![]() .若抛物线
.若抛物线![]() 与直线
与直线![]() 只有一个交点
只有一个交点![]() ,已知点
,已知点![]() 在第一象限,且
在第一象限,且![]() ,令
,令![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方法回顾)
课本研究三角形中位线性质的方法
已知:如图①, 已知![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 两边中点.
两边中点.
求证:![]() ,
,![]()
证明:延长![]() 至点
至点![]() ,使
,使![]() , 连按
, 连按![]() .可证:
.可证:![]() ( )
( )
由此得到四边形![]() 为平行四边形, 进而得到求证结论
为平行四边形, 进而得到求证结论
(1)请根据以上证明过程,解答下列两个问题:
①在图①中作出证明中所描述的辅助线(请用![]() 铅笔作辅助线);
铅笔作辅助线);
②在证明的括号中填写理由(请在![]() ,
,![]() ,
,![]() ,
,![]() 中选择) .
中选择) .
(问题拓展)
(2)如图②,在等边![]() 中, 点
中, 点![]() 是射线
是射线![]() 上一动点(点
上一动点(点![]() 在点
在点![]() 的右侧),把线段
的右侧),把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() 、
、![]() .
.
①请你判断线段![]() 与
与![]() 的数量关系,并给出证明;
的数量关系,并给出证明;
②若![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
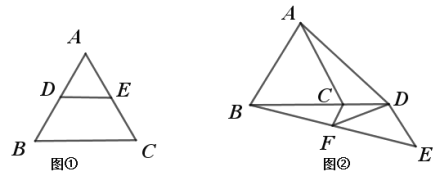
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
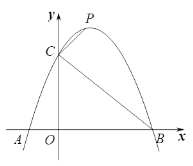
查看答案和解析>>
科目:初中数学 来源: 题型:
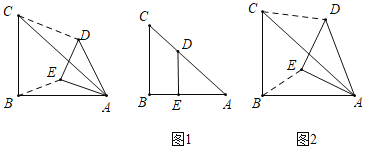
【题目】定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在![]() 与
与![]() 中,
中,![]() ,且
,且![]() 所以称
所以称![]() 与
与![]() 为“关联等腰三角形”,设它们的顶角为
为“关联等腰三角形”,设它们的顶角为![]() ,连接
,连接![]() ,则称
,则称![]() 会为“关联比".
会为“关联比".
下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:
[特例感知]
![]() 当
当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,
时,
①在图1中,若点![]() 落在
落在![]() 上,则“关联比”
上,则“关联比”![]() =
=
②在图2中,探究![]() 与
与![]() 的关系,并求出“关联比”
的关系,并求出“关联比”![]() 的值.
的值.

[类比探究]
![]() 如图3,
如图3,
①当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() =
=
②猜想:当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() = (直接写出结果,用含
= (直接写出结果,用含![]() 的式子表示)
的式子表示)
[迁移运用]
![]() 如图4,
如图4, ![]() 与
与![]() 为“关联等腰三角形”.若
为“关联等腰三角形”.若![]() 点
点![]() 为
为![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 为
为![]() 上一动点,求点
上一动点,求点![]() 自点
自点![]() 运动至点
运动至点![]() 时,点
时,点![]() 所经过的路径长.
所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com