【题目】如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE=OC，连接CE、OE，连接AE交OD于点F．
（1）求证：OE=CD；
（2）若菱形ABCD的边长为4，∠ABC=60°，求AE的长．
科目：初中数学 来源： 题型：
【题目】如图，过A点的一次函数的图象与正比例函数y＝2x的图象相交于点B.
(1)求一次函数的解析式；
(2)判断点C(4，－2)是否在该一次函数的图象上，说明理由；
(3)若该一次函数的图象与x轴交于D点，求△BOD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知， 
， 
与
成正比例， 
与
成反比例，并且当
时， 
，当
时， 
．
（
）求
关于
的函数关系式．
（
）当
时，求
的值．
【答案】（
）
；（
）
， 
．
【解析】分析：（1）首先根据
与x成正比例， 
与x成反比例，且当x=1时，y=4；当x=2时，y=5，求出
和
与x的关系式，进而求出y与x的关系式，（2）根据（1）问求出的y与x之间的关系式，令y=0，即可求出x的值．
本题解析：
（
）设
， 
，
则
，
∵当
时， 
，当
时， 
，
∴
解得， 
，
∴
关于
的函数关系式为
．
（
）把
代入
得，
，
解得： 
， 
．
点睛：本题考查了用待定系数法求反比例函数的解析式：（1）设出含有待定系数的反比例函数解析式y=kx(k为常数，k≠0);(2)把已知条件（自变量与对应值）代入解析式，得到待定系数的方程；（3）解方程，求出待定系数；（4）写出解析式.
【题型】解答题
【结束】
24
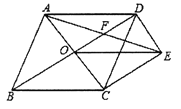
【题目】如图，菱形
的对角线
、
相交于点
，过点
作
且
，连接
、
，连接
交
于点
.
(1)求证:
;
(2)若菱形的边长为2, 
.求的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，完成下列各题：平面内的两条直线有相交和平行两种位置关系。
（1）如图1，若
，点P在AB，CD之间，求证：∠BPD=∠B+∠D；
（2）在图1中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图2，请写出
，∠B，
，
之间的数量关系并说明理由；
（3）利用（2）的结论，求图3中
+∠G=n×90°，则n=____.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为保护环境，增强居民环保意识，某校积极参加即将到来的6月5日的“世界环境日”宣传活动，七年级（1）班所有同学在同一天调查了各自家庭丢弃塑料袋的情况，统计结果的条形统计图如下：
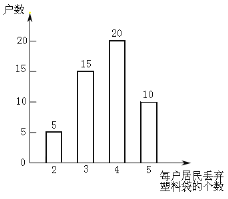
根据统计图，请回答下列问题：
（1）这组数据共调查了居民有多少户?
（2）这组数据的居民丢弃塑料袋个数的中位数是_______个，众数是 _______个.
（3）该校所在的居民区约有3000户居民，估计该居民区每天丢弃的塑料袋总数大约是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某企业积极响应政府“创新发展”的号召，研发了一种新产品．已知研发、生产这种产品的成本为30元/件，且年销售量y(万件)关于售价x(元/件)的函数解析式为：
(1)若企业销售该产品获得的利润为W(万元)，请直接写出年利润W(万元)关于售价x(元/件)的函数解析式；
(2)当该产品的售价x(元/件)为多少时，企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元，试确定该产品的售价x(元/件)的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
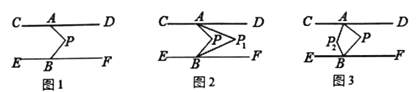
【题目】如图1,已知直线CD//EF ,点A、B分别在直线CD与EF上。P为两平行线间一点
(1)若∠DAP= 40° , ∠FBP=70°,求∠APB的度数是多少?
(2)直接写出∠DAP, ∠FBP, ∠APB之间有什么关系?
(3)利用(2)的结论解答：
①如图2, AP1、BP1,分别平分∠DAP,∠FBP,请你写出∠P与∠P1,的数量关系，并说明理由；
②如图3, AP2、 BP2分别平分∠CAP,∠EBP,若∠APB=β,求∠AP2B (用含β的代数式表示).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了争创全国文明卫生城市，优化城市环境，某市公交公司决定购买10辆全新的混合动力公交车，现有
两种型号，它们的价格及年省油量如下表：
型 号 |
|
|
价格（万元/辆） |
|
|
年省油量（万升/辆） | 2.4 | 2 |
经调查，购买一辆
型车比购买一辆
型车多20万元，购买2辆型车比购买3辆型车少60万元.
（1）请求出
和
的值；
（2）若购买这批混合动力公交车（两种车型都要有）， 每年能节省的油量不低于22.4万升，请问有几种购车方案？（不用一一列出）请求出最省钱的购车方案所需的车款.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
