
【题目】在平面直角坐标系中,![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() ,线段
,线段![]() ,线段
,线段![]() ,且
,且![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,连接
,连接![]() .
.

(1)如图1,在线段![]() 上有两个动点
上有两个动点![]() (
(![]() 在
在![]() 上方),且
上方),且![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]()
![]() 的值最小时,求出
的值最小时,求出![]() 的坐标及
的坐标及![]() 的面积.
的面积.
(2)![]() 沿
沿![]() 轴平移,当点
轴平移,当点![]() 平移到
平移到![]() 边上时,平移后的
边上时,平移后的![]() ,在
,在![]() 轴上一动点
轴上一动点![]() ,在平面直角坐标系内有一动点
,在平面直角坐标系内有一动点![]() ,使点
,使点![]() 形成的四边形为菱形,若存在直接写出点
形成的四边形为菱形,若存在直接写出点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
【答案】(1)P(![]() ,-3
,-3![]() ),
),![]() 的面积=2
的面积=2![]() ;(2)(12,-2
;(2)(12,-2![]() )或(8,2
)或(8,2![]() )或(8+4
)或(8+4![]() ,-2
,-2![]() )
)
【解析】
(1)先根据直角三角形的性质求出OE=2![]() ,由勾股定理得BE=4
,由勾股定理得BE=4![]() ,得出∠ABE=30°,∠EBC=90°,作点F关于EB的对称点H,过H作HP⊥CD于P,交BE于K,交AB于M,则KH=KF,HP的长即KF+KP 的最小值,此时
,得出∠ABE=30°,∠EBC=90°,作点F关于EB的对称点H,过H作HP⊥CD于P,交BE于K,交AB于M,则KH=KF,HP的长即KF+KP 的最小值,此时![]()
![]() 的值最小,由(
的值最小,由(![]() 在
在![]() 上方),且
上方),且![]() 可得出此时点G于点B重合,根据直角三角形的性质求出HP、HM、HK、MK、MG的长,即可解答本题;
可得出此时点G于点B重合,根据直角三角形的性质求出HP、HM、HK、MK、MG的长,即可解答本题;
(2)![]() 沿
沿![]() 轴平移,当点
轴平移,当点![]() 平移到
平移到![]() 边上时,平移后的
边上时,平移后的![]() 中
中![]() 与B重合,分三种情况:①
与B重合,分三种情况:①![]() 为对角线时,②
为对角线时,②![]() 为对角线时,③
为对角线时,③![]() 为对角线时,分别画出图形,利用菱形的性质,直角三角形的性质等知识一一求解即可.
为对角线时,分别画出图形,利用菱形的性质,直角三角形的性质等知识一一求解即可.
解:(1)由题意得OA=2,则OB=6,
∵![]() ,
,
∴∠AEO=30°,OE=2![]() ,
,
Rt△OBE中,BE=![]() =4
=4![]() ,
,
∴∠ABE=30°,
∵![]() ,
,![]() ,
,
∴∠ABC=180°-∠BAD =120°,∠C=60°,AD=BC=6
∴∠EBC=90°,EB⊥BC,
作点F关于EB的对称点H,过H作HP⊥CD于P,交BE于K,交AB于M,则KH=KF,HP的长即KF+KP 的最小值,此时![]()
![]() 的值最小,
的值最小,

∵ HP⊥CD,∠C=60°
∴∠H=30°
∵点![]() 为
为![]() 中点,BC=6,点F关于EB的对称点H,
中点,BC=6,点F关于EB的对称点H,
∴HG=3,CH=9,
在Rt△CPH,Rt△HBK,Rt△HBM中,
HP=![]() ,
,![]() ,KH=2
,KH=2![]() ,BM=
,BM=![]() ,HM=
,HM=![]() ,
,
∴MP=HP-HM=3![]() ,OM=OB-BM=
,OM=OB-BM=![]() ,MK=HK-HM=
,MK=HK-HM=![]() ,
,
∴P的坐标(![]() ,-3
,-3![]() );
);
∵线段![]() 上有两个动点
上有两个动点![]() (
(![]() 在
在![]() 上方),且
上方),且![]() ,
,![]() ,
,
∴此时点G于点B重合,
∴![]() 的面积=
的面积=![]() AGKM=
AGKM=![]() ×8×
×8×![]() =2
=2![]() ;
;
胡答案为:P(![]() ,-3
,-3![]() ),
),![]() 的面积=2
的面积=2![]() ;
;
(2)①如图,![]() 为对角线时,作NH⊥AB与H,由题意得A1B1=8,E1B1=4
为对角线时,作NH⊥AB与H,由题意得A1B1=8,E1B1=4![]() ,∠B1A1E1=60°,∠A1B1E1=30°,E1A1=4,
,∠B1A1E1=60°,∠A1B1E1=30°,E1A1=4,

∵菱形![]()
∴∠A1B1N=60°,∠A1ME1=∠MA1E1=60°,
∴ME1= A1E1=B1N=4,
∴HB1=2,HN=2![]() ,
,
∴OH=OB1-HB1=12,
∴点![]() 的坐标(12,-2
的坐标(12,-2![]() );
);
②![]() 为对角线时,
为对角线时,

∵菱形![]()
∴∠E1B1N=60°,NE1=B1E1=4![]() , HE1=HN=2
, HE1=HN=2![]() ,
,
∴HB1=6,
∴OH=OB1-HB1=8,
∴点![]() 的坐标(8,2
的坐标(8,2![]() );
);
![]() 为对角线时,作NH⊥AB与H,
为对角线时,作NH⊥AB与H,

由题意得∠B1MN=30°,MN=B1E1=B1M=4![]() ,
,
∴HM=6,HN=2![]() ,
,
∴B1H=4![]() -6,
-6,
∴OH=OB1+HB1=14+(4![]() -6)=8+4
-6)=8+4![]() ,
,
∴点![]() 的坐标(8+4
的坐标(8+4![]() ,-2
,-2![]() ).
).
故点![]() 的坐标为:(12,-2
的坐标为:(12,-2![]() )或(8,2
)或(8,2![]() )或(8+4
)或(8+4![]() ,-2
,-2![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知点P,Q为平面直角坐标系xOy中不重合的两点,以点P为圆心且经过点Q作⊙P,则称点Q为⊙P的“关联点”,⊙P为点Q的“关联圆”.
(1)已知⊙O的半径为1,在点E(1,1),F(﹣![]() ,
,![]() ),M(0,-1)中,⊙O的“关联点”为______;
),M(0,-1)中,⊙O的“关联点”为______;
(2)若点P(2,0),点Q(3,n),⊙Q为点P的“关联圆”,且⊙Q的半径为![]() ,求n的值;
,求n的值;
(3)已知点D(0,2),点H(m,2),⊙D是点H的“关联圆”,直线y=﹣![]() x+4与x轴,y轴分别交于点A,B.若线段AB上存在⊙D的“关联点”,求m的取值范围.
x+4与x轴,y轴分别交于点A,B.若线段AB上存在⊙D的“关联点”,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为K90的化学赛道,其中助滑坡AB长90米,坡角a=40°,一个曲面平台BCD连接了助滑坡AB与着陆坡,某运动员在C点飞向空中,几秒之后落在着陆坡上的E处,已知着陆坡DE的坡度i=1: ![]() ,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)
,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)

A. 101.4 B. 101.3 C. 100.4 D. 100.3
查看答案和解析>>
科目:初中数学 来源: 题型:
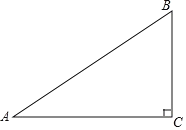
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在坐标平面内△ABC的顶点坐标分别为A(0,2),B(3,3),C(2,1),(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC关于原点对称的△A1B1C1,并直接写出点C1点的坐标;
(2)画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(![]() )
)![]() ,正六边形的边长为(
,正六边形的边长为(![]() )cm(其中
)cm(其中![]() ),求这两段铁丝的总长
),求这两段铁丝的总长

查看答案和解析>>
科目:初中数学 来源: 题型:
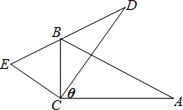
【题目】如图,△ABC中,∠ACB=90°,∠A=25°,若以点C为旋转中心,将△ABC旋转θ度到△DEC的位置,使点B恰好落在边DE上,则θ等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
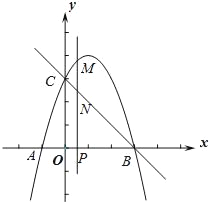
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
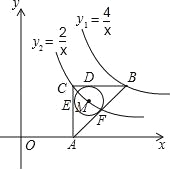
【题目】如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=![]() 的图象经过点B;反比例函数y2=
的图象经过点B;反比例函数y2=![]() 的图象经过点C(
的图象经过点C(![]() ,m).
,m).
(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com