Question

证明题：
（1）如图1，AD⊥BC，EF⊥BC，垂足分别为D，F．又已知∠1=∠2．求证：AB∥GD；

（2）如图2，AB∥CD，∠1：∠2：∠3=1：2：3，判断BA是否平分∠EBF，并证明你的结论．

Answer 1

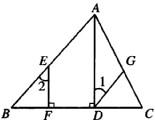
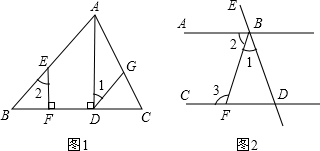
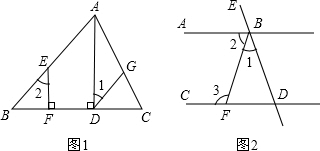
解：（1）证明：∵AD⊥BC，EF⊥BC（已知）
∴∠EFB=∠ADB=90°（垂直的定义）
∴EF∥AD（同位角相等，两直线平行）
∴∠2=∠BAD（两直线平行，同位角相等）
∵∠1=∠2，（已知）
∴∠1=∠BAD（等量代换）
∴AB∥DG．（内错角相等，两直线平行）

（2）判断：BA平分∠EBF
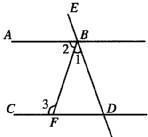
证明：∵∠1：∠2：∠3=1：2：3
∴可设∠1=k，∠2=2k，∠3=3k（k＞0）
∵AB∥CD
∴∠2+∠3=180°
∴2k+3k=180°
∴k=36°
∴∠1=36°，∠2=72°
∴∠ABE=72°（平角定义）
∴∠2=∠ABE
∴BA平分∠EBF（角平分线定义）．
分析：（1）要证明AB∥GD，只要证明∠1=∠BAD即可，根据∠1=∠2，只要再证明∠2=∠BAD即可证得；
（2）根据AB∥CD，∠1：∠2：∠3=1：2：3即可求得三个角的度数，再根据∠EBA与∠ABD互补，可求得∠EBA的度数，即可作出判断．
点评：本题主要考查了平行线的性质，两直线平行，同旁内角互补，内错角相等，以及平行线的判定方法．