
如图,在坐标系中,菱形ABCD的边BC与x轴重合,点B与原点重合,AB=10, ∠ABC=60°.动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动;动点Q从点D出发沿折线DC-CB-BA以每秒3个单位长的速度匀速运动,过点P作PF⊥BC,交折线AB-AC于点E,交直线AD于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之停止,设运动时间为t秒.
(1)写出点A与点D的坐标
(2)当t=3秒时,试判断QE与AB之间的位置关系?
(3)当Q在线段DC上运动时,若△PQF为等腰三角形,求t的值;
(4)设△PQE的面积为S,求S与t的函数关系式;

(1) A(5,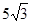 )
D(15,
)
D(15,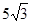 )
)
(2) 当t=3时,EQ⊥ AB
过A作AM//EQ,
∵BP=3时,∠B=60°∴BE=6,
∴AE=10-6=4,
∴AE=QM=4,
∴DM=3×3-4=5,
∴DM=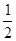 AD,又∵∠ADC=60°,
AD,又∵∠ADC=60°,
∴∠AMD=90°,
∴∠AEQ=90°,
∴EQ⊥AB。
(3)P点坐标为(t,0),F坐标为(t, 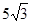 ),Q(
),Q(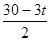 ,
, )
)
(1)当FQ=PQ时,t=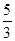
(2)当PF=FQ时, ,
,
∴t1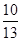 ,t2=5(舍)
,t2=5(舍)
(3)当PF=PQ时 ,
,
∴t1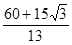 (舍),t2=
(舍),t2=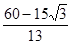 ,
,
∴当t= 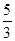 或
或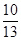 或
或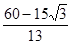 时,△PQF为等腰△。
时,△PQF为等腰△。
(4)0∠t≤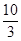 时,
时,
S=10×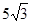 -
-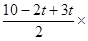
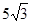 -
-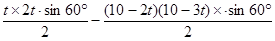
=-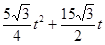 ,
,
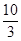 <t≤5时,
<t≤5时,
S=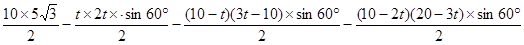
=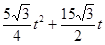 +
+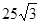
5<t<6时,
S=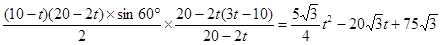
6<t时≤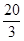 ,
,
S=
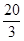 <t≤10,
<t≤10,
S=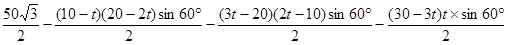
=-
【解析】(1)利用菱形的边角关系求出A、D点坐标;
(2)过A作AM//EQ,先算出DM的长,然后根据边角的关系得出∠AMD=90°,再根据四边形AEQM是平行四边形得出∠AEQ=90°,从而得出EQ⊥AB。
(3)分PF=FQ、FQ=PQ、PF=PQ三种情况进行讨论;
(4)分五种情况进行讨论。


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源:2010--2011学年度山东潍坊市四县市七年级第二学期期末质量监测数学 题型:解答题
(11·贺州)(本题满分6分)
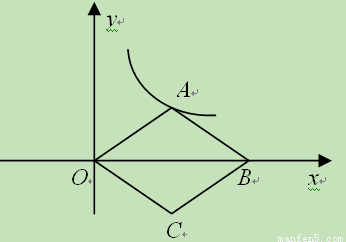
如图,在平面直角坐标系中,点O为原点,反比例函数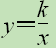 的图象经过点(1,4),菱
的图象经过点(1,4),菱
形OABC的顶点A在函数的图象上,对角线OB在x轴上.
(1)求反比例函数的关系式;
(2)直接写出菱形OABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com