解:(1)由△AOC∽△COB,可得OC
2=OA×OB=36,
∴OC=6
又∵点C在y轴的正半轴上,
∴点C的坐标是(0,6);
(2)过点D作DE⊥BC于点E.设DB的长为m.
在Rt
△DEB中,DE=DB•sinB=m•

=

m,BE=DB•cosB=

m
在Rt
△DEC中,∠DEC=45°,于是CE=DE=

m
由CE+BE=BC,即

m+

m=3

,解得m=5
又由OA>OB,知点D在线段OA上,OB=3,所以OD=2,故点D(-2,0);
设直线l的解析式为:y=kx+b,把C(0,6)和D(-2,0)代入y=kx+b中,
得
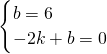
,
解得
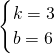
.
故直线l的解析式为:y=3x+6;
(3)①取AB的中点F(-4.5,0),过点F作BC的平行线交直线l于点P
1,连接CF.
易知S
△P1BC=S
△FBC=S
△ACB,∴点P
1为符合题意的点.
直线P
1F可由直线BC向左平移BF个单位得到(即向左平移7.5个单位)
而直线BC的解析式为y=-2x+6,
即直线P
1F的解的式为y=-2(x+7.5)+6即
y=-2x-9,由
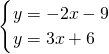
得点P
1(-3,-3)
②在直线l上取点P
2使C P
2=C P
1,此时有S
△P2BC=S
△P1BC=

S
△ACB,∴点符P
2合题意.
由C P
2=C P
1,可得点P
2的坐标为(3,15),∴点P(-3,-3)或P(3,15)可使S
△PBC=

S
△APBC;
(4)当OC是菱形的对角线时,OC的中点的坐标是(0,3),则把y=3代入l的解析式得:3x+6=3,
解得:x=-1.
则M的坐标是(-1,3),N的坐标是(1,3);
当OC是菱形的一条边时,点N的坐标是(-

,-

),(

,

),(-

,-

).
故N的坐标是(1,3)或(-

,-

)或(

,

)或(-

,-

).
分析:(1)OC是直角△ABC斜边上的高线,则△AOC∽△COB,根据相似三角形的对应边的比相等,即可求得OC的长,进而求得C的坐标;
(2)过点D作DE⊥BC于点E.设DB的长为m,在直角△BDE中,利用三角函数利用m表示出DE和BE的长,进而表示出CE的长,根据BE+CE=BC即可得到一个关于m的方程求得m的值,则D的横坐标即可求解,然后利用待定系数法即可求得函数的解析式;
(3)延长AB到Q使BG=

AB,根据S
△PBC=

S
△ABC则点P一定在经过AB的中点或Q平行于直线BC的直线上,这条直线与l的交点就是P点;
(4)当OC是菱形的对角线时,MN一定在AC的中垂线上,且MN一定关于OC对称,据此即可求得N的坐标;
当OC是菱形的一条边时,依据M在直线l上,即可求得M的坐标,再由MN∥OC,MN=OC即可得出N点坐标.
点评:本题是待定系数法求函数的解析式,以及三角形的面积,直线平行的条件,菱形的性质的综合应用,正确进行讨论是关键.

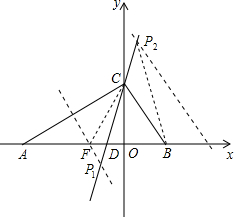
 如图,已知点A(-12,0),B(3,0),点C在y轴的正半轴上,且∠ACB=90°.
如图,已知点A(-12,0),B(3,0),点C在y轴的正半轴上,且∠ACB=90°. S△ABC的点P的坐标;
S△ABC的点P的坐标; =
= m,BE=DB•cosB=
m,BE=DB•cosB= m
m m
m m+
m+ m=3
m=3 ,解得m=5
,解得m=5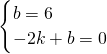 ,
,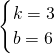 .
.
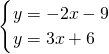 得点P1(-3,-3)
得点P1(-3,-3) S△ACB,∴点符P2合题意.
S△ACB,∴点符P2合题意. S△APBC;
S△APBC; ,-
,- ),(
),( ,
, ),(-
),(- ,-
,- ).
). ,-
,- )或(
)或( ,
, )或(-
)或(- ,-
,- ).
). AB,根据S△PBC=
AB,根据S△PBC= S△ABC则点P一定在经过AB的中点或Q平行于直线BC的直线上,这条直线与l的交点就是P点;
S△ABC则点P一定在经过AB的中点或Q平行于直线BC的直线上,这条直线与l的交点就是P点;

 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设