
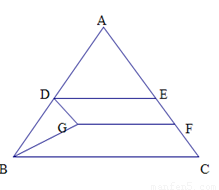
如图,在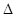
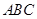 中,
中,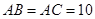 ,
,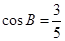 ,点
,点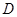 在
在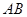 边上(点
边上(点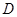 与点
与点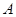 、
、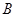 不重合),
不重合),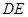 ∥
∥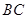 交
交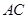 边与点
边与点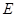 ,点
,点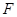 在线段
在线段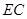 上,且
上,且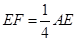 ,以
,以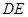 、
、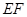 为邻边作平行四边形
为邻边作平行四边形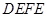 联结
联结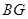 .
.
(1)当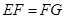 时,求
时,求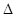
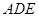 的面积;
的面积;
(2)设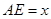 ,
,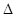
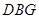 的面积为
的面积为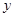 ,求
,求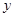 与
与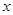 的函数关系式,并写出
的函数关系式,并写出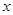 的取值范围;
的取值范围;
(3)如果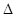
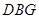 是以
是以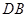 为腰的等腰三角形,求
为腰的等腰三角形,求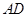 的值.
的值.
(1)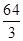 (2)
(2)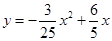

 (3)
(3)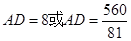
【解析】(1)作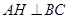 于
于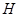 ,在
,在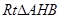 中,
中,
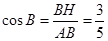
∵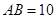 ,
,
∴ ,
,
∴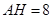
∵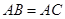 ,
,
∴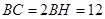 ,
,
∴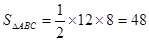 (1分)
(1分)
∵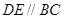 ,∴
,∴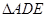 ∽
∽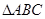 ,
,
∴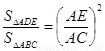 (1分)
(1分)
∵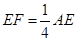 ,
, 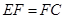 ,
,
∴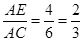 ,
(1分)
,
(1分)
∴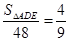 ,
,
∴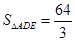 (1分)
(1分)
解:(2)设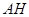 交
交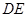 、
、 于点
于点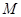 、
、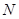
∵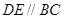 ,
,
∴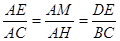
∵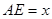 ,
,
∴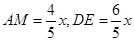 (1分)
(1分)
∵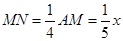 ,
,
∴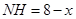 (1分)
(1分)
∴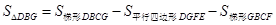
∴ 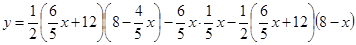
∴ 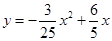

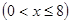 (2分)
(2分)
解:(3)作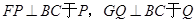
在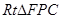 中,
中,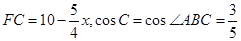
∴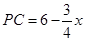 ,
,
∴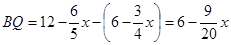
∴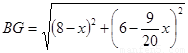 (2分)
(2分)
在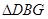 中,
中,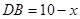 ,
,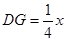
①若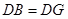 ,则
,则 ,解得
,解得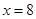 (2分)
(2分)
②若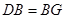 ,则
,则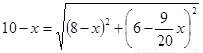
解得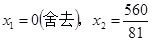 (2分)
(2分)
∴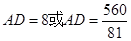
(1)作AH⊥BC于H,在Rt△AHB中,cosB= 可得出AH、BC的长,进而可得出△ABC的面积,由相似三角形的判定定理得出△ADE∽△ABC,根据相似三角形面积的比等于相似比即可得出△ADE的面积;
可得出AH、BC的长,进而可得出△ABC的面积,由相似三角形的判定定理得出△ADE∽△ABC,根据相似三角形面积的比等于相似比即可得出△ADE的面积;
(2)设AH交DE、GF于点M、N,由(1)可知△ADE∽△ABC,故可得出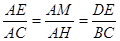 ,再根据AE=x,可知AM=4/5x,DE=6/5x,NH=8-x,根据S△DBG=S梯形DBCE-S平行四边形DGFE-S梯形GBCF,即可得出结论;
,再根据AE=x,可知AM=4/5x,DE=6/5x,NH=8-x,根据S△DBG=S梯形DBCE-S平行四边形DGFE-S梯形GBCF,即可得出结论;
(3)作FP⊥BC于P,GQ⊥BC于Q,由FC=10-5/4 x,cosC=cos∠ABC=3/5,可知PC=6-3/4 x,BQ=12-6/5 x-(6-3/4x)=6-9/20 x,由勾股定理可用x表示出BG的长,在△DBG中用x表示出DB,DG的长,再分DB=DG和DB=BG两种情况进行讨论.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
 请求出此值;若变化,请说明理由.
请求出此值;若变化,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | 2 |
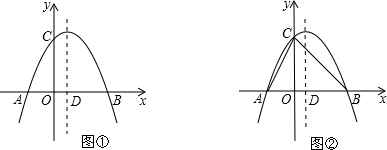
查看答案和解析>>
科目:初中数学 来源: 题型:
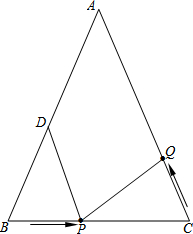 如图,在△ABC中,AB=AC=20cm,BC=16cm,点D是AB边的中点.点P是BC边上的动点,以3cm/秒的速度从点B向点C运动;点Q是AC边上的动点,同时从点C向点A运动.设运动时间为t cm/秒.
如图,在△ABC中,AB=AC=20cm,BC=16cm,点D是AB边的中点.点P是BC边上的动点,以3cm/秒的速度从点B向点C运动;点Q是AC边上的动点,同时从点C向点A运动.设运动时间为t cm/秒.查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海市徐汇初三二模数学试卷(解析版) 题型:解答题
如图,在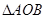 中,点
中,点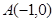 ,点
,点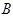 在
在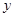 轴正半轴上,且
轴正半轴上,且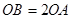 .
.

(1)求点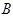 的坐标;
(3分)
的坐标;
(3分)
(2)将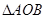 绕原点
绕原点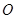 顺时针旋转
顺时针旋转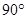 ,点
,点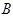 落在
落在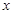 轴正半轴的点
轴正半轴的点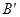 处,抛物线
处,抛物线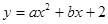 经过点
经过点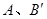 两点,求此抛物线的解析式及对称轴.(7分)
两点,求此抛物线的解析式及对称轴.(7分)
查看答案和解析>>
科目:初中数学 来源:2012届上海市徐汇初三二模数学试卷(带解析) 题型:解答题
如图,在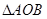 中,点
中,点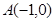 ,点
,点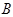 在
在 轴正半轴上,且
轴正半轴上,且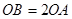 .
.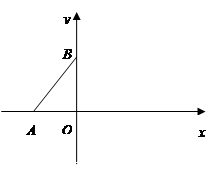
(1)求点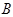 的坐标; (3分)
的坐标; (3分)
(2)将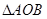 绕原点
绕原点 顺时针旋转
顺时针旋转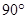 ,点
,点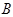 落在
落在 轴正半轴的点
轴正半轴的点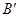 处,抛物线
处,抛物线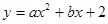 经过点
经过点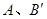 两点,求此抛物线的解析式及对称轴.(7分)
两点,求此抛物线的解析式及对称轴.(7分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com