
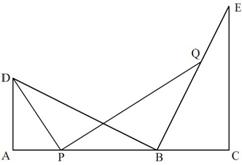
如图,点![]() 在线段
在线段![]() 上,点
上,点![]() ,
,![]() 在
在![]() 同侧,
同侧,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,连接
上的动点,连接![]() ,作
,作![]() ,交直线
,交直线![]() 与点
与点![]() ;
;
i)当点![]() 与
与![]() ,
,![]() 两点不重合时,求
两点不重合时,求![]() 的值;
的值;
ii)当点![]() 从
从![]() 点运动到
点运动到![]() 的中点时,求线段
的中点时,求线段![]() 的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
科目:初中数学 来源: 题型:
| 4 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012年浙教版初中数学九年级上4.3两个三角形相似的判定练习卷(解析版) 题型:解答题
已知:如图,点 在线段
在线段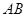 上,
上, 是等边三角形.(1)当
是等边三角形.(1)当 满足怎样的关系式时
满足怎样的关系式时 ;(2)当
;(2)当 时,求
时,求 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海市浦东新区初三二模数学试卷(解析版) 题型:解答题
已知:正方形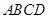 的边长为1,射线
的边长为1,射线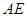 与射线
与射线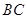 交于点
交于点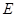 ,射线
,射线 与射线
与射线 交于点
交于点 ,
,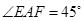 .
.
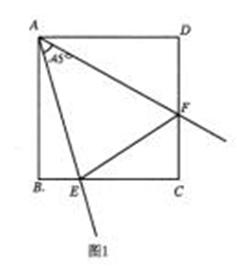
(1)如图1,当点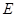 在线段
在线段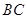 上时,试猜想线段
上时,试猜想线段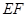 、
、 、
、 有怎样的数量关系?并证明你的猜想.
有怎样的数量关系?并证明你的猜想.
(2)设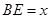 ,
, ,当点
,当点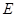 在线段
在线段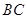 上运动时(不包括点
上运动时(不包括点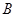 、
、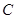 ),如图 1,求
),如图 1,求 关于
关于 的函数解析式,并指出
的函数解析式,并指出 的取值范围.
的取值范围.
(3)当点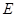 在射线
在射线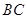 上运动时(不含端点
上运动时(不含端点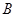 ),点
),点 在射线
在射线 上运动.试判断以
上运动.试判断以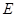 为圆心以
为圆心以 为半径的
为半径的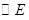 和以
和以 为圆心以
为圆心以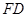 为半径的
为半径的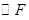 之间的位置关系.
之间的位置关系.

(4)当点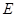 在
在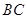 延长线上时,设
延长线上时,设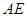 与
与 交于点
交于点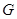 ,如图 2.问△
,如图 2.问△ 与△
与△ 能否相似,若能相似,求出
能否相似,若能相似,求出 的值,若不可能相似,请说明理由.
的值,若不可能相似,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com