
如图,直线 分别与两坐标轴交于A,B两点,点C从A点出发沿射线BA方向移动,速度为每秒1个单位长度.以C为顶点作等边△CDE,其中点D和点E都在x轴上.半径为
分别与两坐标轴交于A,B两点,点C从A点出发沿射线BA方向移动,速度为每秒1个单位长度.以C为顶点作等边△CDE,其中点D和点E都在x轴上.半径为 的⊙M与x轴、直线AB相切于点G、F.
的⊙M与x轴、直线AB相切于点G、F.

(1)直线AB与x轴所夹的角∠ABO= °;
(2)求当点C移动多少秒时,等边△CDE的边CE与⊙M相切?
(1)30;(2)4或 .
.
【解析】
试题分析:(1)根据直线解析式求出OA、OB的长度,再由∠ABO的正切值,可求出∠AOB的度数:直线AB的解析式为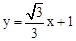 ,令x=0,则y=1,令y=0,则
,令x=0,则y=1,令y=0,则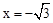 ,∵
,∵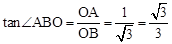 ,∴∠ABO=30°;(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.
,∴∠ABO=30°;(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.
试题解析:(1)30;
(2)设点C移动t秒后与⊙M相切,
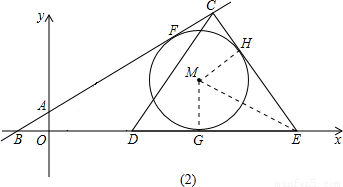
①当CE在⊙M左侧相切于点H,如图(1),连接MF、MG、MH,
∵AB、CE、BO均为⊙M的切线,∴MF⊥AB,MH⊥CE,MG⊥BO.
∵∠ABO=30°,△CDE是等边三角形,∴∠BCE=90°. ∴四边形CHMF为矩形.
∵MF=MH,∴四边形CHMF为正方形. ∴CH=MH=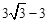 .
.
∵EH、EG为⊙M的切线,∠CED=60°,∴∠HEM=60°. ∴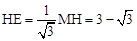 .
.
∵ ,∴
,∴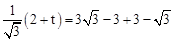 ,解得t=4.
,解得t=4.

②当CE在⊙M右侧相切于点H(如图(2)),
由①证得:CH=MH=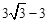 .
.
∵∠HEM=30°,∴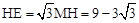 .
.
∴ ,解得,t=
,解得,t= .
.
考点:1.圆的综合题;2.动点问题;3.锐角三角函数定义;4.特殊角的三角函数值;5.切线的性质;6. 等边三角形的性质;7. 正方形的判定和性质;8.分类思想的应用.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
|
|
|

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是
(2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:044
如图,在直角坐标系中,O是原点,A、B、C三点的坐标分别为A(18,0),B(18,6),C(8,6),四边形OABC是梯形,点P、Q同时从原点出发,分别坐匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位,点Q沿OC、CB向终点B运动,当这两点有一点到达自己的终点时,另一点也停止运动。
⑴ 求出直线OC的解析式及经过O、A、C三点的抛物线的解析式。
⑵ 试在⑴中的抛物线上找一点D,使得以O、A、D为顶点的三角形与△AOC全等,请直接写出点D的坐标。
⑶ 设从出发起,运动了t秒。如果点Q的速度为每秒2个单位,试写出点Q的坐标,并写出此时t的取值范围。
⑷ 设从出发起,运动了t秒。当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半,这时,直线PQ能否把梯形的面积也分成相等的两部分,如有可能,请求出t的值;如不可能,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
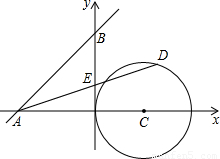
 如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是________.
如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是________.查看答案和解析>>
科目:初中数学 来源:2012年山东省济南市历下区中考数学二模试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com