
 的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB =" 2OC=" 3.
的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB =" 2OC=" 3.
 DQ,试求出y2关于x的函数关系式;
DQ,试求出y2关于x的函数关系式; 分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为
分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为 ?若能,求出m的值;若不能,请说明理由.
?若能,求出m的值;若不能,请说明理由. 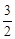 )两点,
)两点,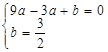 ,∴
,∴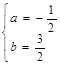
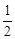 x2+x+
x2+x+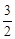 . ---------4分
. ---------4分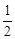 x2+x+
x2+x+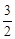 易得D(1,2), N(1,0),A(-1,0),B(3,0),
易得D(1,2), N(1,0),A(-1,0),B(3,0),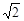 ,
,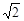 )2-22=PD2-(1-x)2-----j
)2-22=PD2-(1-x)2-----j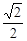 y2´2
y2´2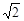 ------k.
------k.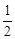 x2-x+
x2-x+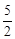 .∵0≤x<3,
.∵0≤x<3,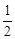 x2-x+
x2-x+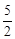 =
=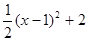
 (0≤x≤3).--------4分
(0≤x≤3).--------4分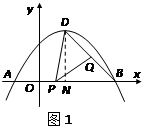

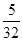 (如图2)
(如图2)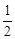 x2+x+
x2+x+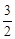 =
=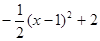 分别与直线x=m,x= m+
分别与直线x=m,x= m+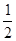 的交点
的交点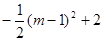 ),G(m+
),G(m+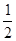 ,
,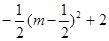 ).
).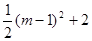 ),H(m+
),H(m+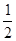 ,
,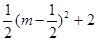 ).
).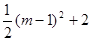 -[
-[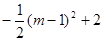 ]=
]=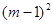
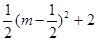 )-[
)-[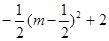 ]=
]=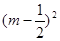 .
.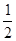 [
[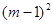 +
+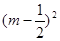 ]×
]×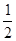 =
=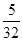
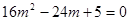
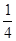 或
或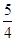 (都在0≤x≤3内)
(都在0≤x≤3内)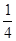 或
或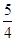 时,E、F、H、G围成四边形的面积为
时,E、F、H、G围成四边形的面积为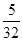 . --------4分解析:
. --------4分解析: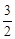 )两点,求出拋物线的解析式,
)两点,求出拋物线的解析式,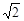 ,由根据勾股定理得jPD2-(1-x)2=4,又因为△MPQ ∽ △MBP,所以kPD2=DQ´DB=
,由根据勾股定理得jPD2-(1-x)2=4,又因为△MPQ ∽ △MBP,所以kPD2=DQ´DB=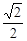 y2´2
y2´2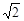 ,由j、k得y2与x的函数关系式
,由j、k得y2与x的函数关系式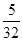 ,通过y1求出E、G、F、H的坐标,求出EF、GH的长度,
,通过y1求出E、G、F、H的坐标,求出EF、GH的长度,

科目:初中数学 来源: 题型:
| 1 | 2 |
 点.
点.查看答案和解析>>
科目:初中数学 来源: 题型:
 21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).
21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为
(2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
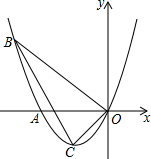 (2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
(2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com