
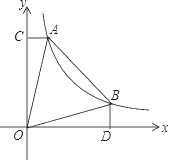
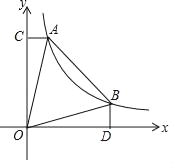
【题目】如图,A、B两点在反比例函数![]() (k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(1)若△AOC的面积为4,求k值;
(2)若a=1,b=k,当AO=AB时,试说明△AOB是等边三角形;
(3)若OA=OB,证明:OC=OD.
【答案】(1)8(2)△AOB是等边三角形(3)见解析
【解析】
(1)由反比例函数系数k的几何意义解答;
(2)根据全等三角形△ACO≌△BDO(SAS)的性质推知AO=BO,结合已知条件AO=AB得到:AO=BO=AB,故△AOB是等边三角形;
(3)证明:在Rt△ACO和Rt△BDO中,根据勾股定理得:AO2=AC2+OC2,BO2=BD2+OD2,结合已知条件OA=OB,得到:AC2+OC2=BD2+OD2,由坐标与图形性质知:![]() ,整理得到:
,整理得到:![]() ,
,![]() ,易得
,易得![]() ,故OC=OD.
,故OC=OD.
解:(1)∵AC⊥y轴于点C,点A在反比例函数![]() (k>0,x>0)的图象上,且△AOC的面积为4,
(k>0,x>0)的图象上,且△AOC的面积为4,
∴![]() |k|=4,
|k|=4,
∴k=8;
(2)由a=1,b=k,可得A(1,k),B(k,1),
∴AC=1,OC=k,OD=k,BD=1,
∴AC=BD,OC=OD.
又∵AC⊥y轴于点C,BD⊥x轴于点D,
∴∠ACO=∠BDO=90°,
∴△ACO≌△BDO(SAS).
∴AO=BO.
又AO=AB,
∴AO=BO=AB,
∴△AOB是等边三角形;
(3)证明:在Rt△ACO和Rt△BDO中,根据勾股定理得:AO2=AC2+OC2,BO2=BD2+OD2,
∵OA=OB,
∴AC2+OC2=BD2+OD2,
即有:![]() ,
,
∴![]() ,
,![]() ,
,
因为0<a<b,所以a2﹣b2≠0,
∴![]() ,
,
∴![]() ,负值舍去,得:
,负值舍去,得:![]() ,
,
∴![]() ,
,
∴OC=OD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,![]() ,顶点C的坐标为
,顶点C的坐标为![]() ,x反比例函数
,x反比例函数![]() 的图象与菱形对角线AO交于点D,连接BD,当
的图象与菱形对角线AO交于点D,连接BD,当![]() 轴时,k的值是______.
轴时,k的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________

查看答案和解析>>
科目:初中数学 来源: 题型:
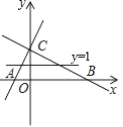
【题目】如图,直线y1=2x+2交x轴、y轴于点A、C,直线![]() 交x轴、y轴于点B、C,点P(m,1)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
交x轴、y轴于点B、C,点P(m,1)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.2B.2.5C.3D.3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
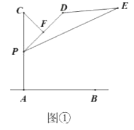
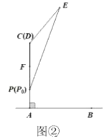
【题目】在炎热的夏季,遮阳伞在我们的生活中随处可见.如图①,滑动调节式遮阳伞的立柱![]() 直于地面
直于地面![]() ,点
,点![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() .当点
.当点![]() 位于初始位置
位于初始位置![]() 时,点
时,点![]() 与
与![]() 重合(如图②).根据生活经验,当太阳光线与
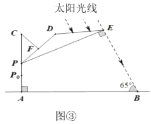
重合(如图②).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.已知太阳光线与地面的夹角为
垂直时,遮阳效果最佳.已知太阳光线与地面的夹角为![]() (如图③),为使遮阳效果最佳,点
(如图③),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少米?(结果精确到
上调多少米?(结果精确到![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
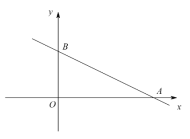
【题目】已知:如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 和点
和点![]() ,并与
,并与![]() 轴相交于另一点
轴相交于另一点![]() ,对称轴与
,对称轴与![]() 轴相交于点
轴相交于点![]() .
.
(1)求抛物线的表达式;
(2)求证:![]() ;
;
(3)如果点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,y=ax2+bx-2的图象过A(1,0),B(-2,0),与y轴交于点C.
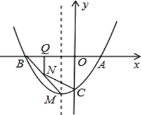
(1)求抛物线关系式及顶点M的坐标;
(2)若N为线段BM上一点,过N作x轴的垂线,垂足为Q,当N在线段BM上运动(N不与点B、点M重合),设NQ的长为t,四边形NQAC的面积为S,求S与t的关系式并求出S的最大值;
(3)在抛物线的对称轴上是否存在点P,使△PAC为直角三角形?若存在,请直接写出所有符合条件P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是甲、乙两个圆柱形水槽,一个圆柱形的空玻璃杯放置在乙槽中(空玻璃杯的厚度忽略不计).将甲槽的水匀速注入乙槽的空玻璃杯中,甲水槽内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2线段DE所示,乙水槽(包括空玻璃杯)内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2折线O﹣A﹣B﹣C所示.记甲槽底面积为S1,乙槽底面积为S2,乙槽中玻璃杯底面积为S3,则S1:S2:S3的值为_______.
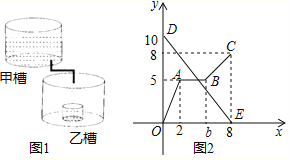
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com