
如下图,在直角坐标系中,已知点M0的坐标为(1,0),将线段OM0绕原点O沿逆时针方向旋转45°,再将其延长到M1,使得M1M0⊥OM0,得到线段OM1;又将线段OM1绕原点O沿逆时针方向旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2,如此下去,得到线段OM3,OM4,……,OMn.
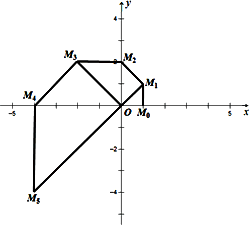
(1)写出点M5的坐标;
(2)求△M5OM6的周长;
(3)我们规定:把点Mn(xn,yn)(n=0,1,2,3……的横坐标xn,纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Mn的“绝对坐标”.根据图中点Mn的分布规律,请你猜想点Mn的“绝对坐标”,并写出来.
|
(1)M5(―4,―4) 4分 (2)由规律可知, ∴ (3)解法一:由题意知, 令旋转次数为 当点M在x轴上时:M0( 即:点 当点M在y轴上时:M2 当点M在各象限的分角线上时:M1 M5 解法二:由题意知, ①当 ②当 |


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
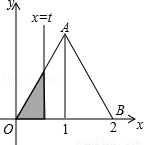
 如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )
如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的性质(带解析) 题型:单选题
如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )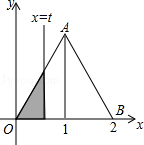
A. | B. | C. | D.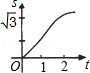 |
查看答案和解析>>
科目:初中数学 来源:2008年江苏省淮安市淮阴中学高一分班考试数学试卷(解析版) 题型:选择题




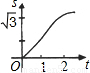
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的性质(解析版) 题型:选择题
如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
如下图,在直角坐标系中,M为![]() 轴上一点,⊙M交
轴上一点,⊙M交![]() 轴于A、B两点,交
轴于A、B两点,交![]() 轴于C、D两点,P为BC上的一个动点,CQ平分∠PCD,A(-1,0),如(1,0)。
轴于C、D两点,P为BC上的一个动点,CQ平分∠PCD,A(-1,0),如(1,0)。
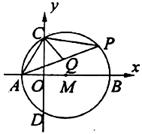
(1)求C点的坐标;
(2)当P点运动时,线段AQ的长度是否改变?若不变,请求其值;若改变请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com