
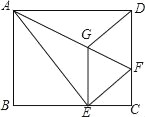
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)试证明EG2=![]() GFAF.
GFAF.
【答案】(1)见解析;(2)见解析.
【解析】
(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF;
(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
(1)证明:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.
(2)解:如图所示:连接DE,交AF于点O.
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO=![]() GF,DF=EG,
GF,DF=EG,
∴EG2=![]() GFAF.
GFAF.


科目:初中数学 来源: 题型:
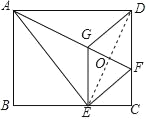
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图像交于点
的图像交于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,且
,且![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图象上.
的图象上.
(1)求![]() 的值;
的值;
(2)在![]() 轴的正半轴上存在一点
轴的正半轴上存在一点![]() ,使得
,使得![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
(3)点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,把
,把![]() 向右平移
向右平移![]() 个单位到
个单位到![]() 的位置,当
的位置,当![]() 取得最小值时,请你在横线上直接写出
取得最小值时,请你在横线上直接写出![]() 的值,
的值,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
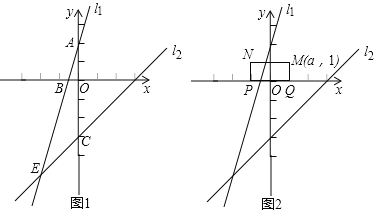
【题目】如图1,在直角坐标系中,一次函数的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图象
的图象![]() 交于点
交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与y轴交于点
与y轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)如图2,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的边
的边![]() 在
在![]() 轴上平移,若矩形
轴上平移,若矩形![]() 与直线
与直线![]() 或
或![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围,
的取值范围,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为测量一棵古树![]() 和教学楼
和教学楼![]() 的高,先在
的高,先在![]() 处用高1.5米的测角仪测得古树顶端
处用高1.5米的测角仪测得古树顶端![]() 的仰角
的仰角![]() 为
为![]() ,此时教学楼顶端
,此时教学楼顶端![]() 恰好在视线
恰好在视线![]() 上,再向前走9米到达
上,再向前走9米到达![]() 处,又测得教学楼顶端
处,又测得教学楼顶端![]() 的仰角
的仰角![]() 为
为![]() ,点
,点![]() 、
、![]() 、
、![]() 三点在同一水平线上.
三点在同一水平线上.
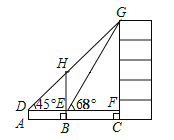
(1)计算古树![]() 的高;
的高;
(2)计算教学楼![]() 的高.(结果精确到0.1米,参考数据:
的高.(结果精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线 ![]() 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
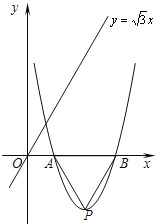
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求该文具店购进A、B两种钢笔每支各多少元?
(2)经统计,B种钢笔售价为30元时,每月可卖64支;每涨价3元,每月将少卖12支,求该文具店B种钢笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某市球类运动协会为了筹备一次大型体育活动,购进了一定数量的体育器材,器材管理员对购买的部分器材进行了统计,表1和图2是器材管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
频率分布表
器材种类 | 频数 | 频率 |
排 球 | 20 | |
乒乓球拍 | 50 | 0.50 |
篮 球 | 25 | 0.25 |
足 球 | ||
合 计 | 1 |
![]()
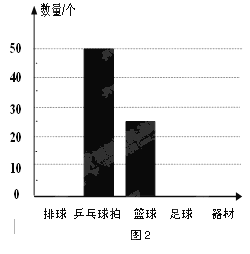
(1)填充图1频率分布表中的空格.
(2)在图2中,将表示“排球”和“足球”的部分补充完整.
(3)已知该协会购买这批体育器材时,篮球和足球一共花去950元,且足球每个的价格比篮球多10元.现准备再采购篮球和足球这两种球共10个(两种球的个数都不能为0),计划资金不超过320元,试问该协会有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com