【题目】如图，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成；…，按照此规律，第n个图中正方形和等边三角形的个数之和为（ ）个．
A.9nB.6nC.9n＋3D.6n+3
能力评价系列答案
唐印文化课时测评系列答案科目：初中数学 来源： 题型：
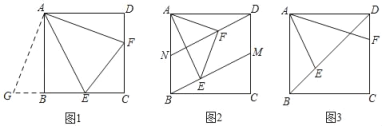
【题目】已知：正方形ABCD，∠EAF＝45°．
（1）如图，当点E、F分别在边BC、CD上，连接EF，求证：EF＝BE+DF；
童威同学是这样思考的，请你和他一起完成如下解答：证明：将△ADF绕点A顺时针旋转90°，得△ABG，所以△ADF≌△ABG．
（2）如图，点M、N分别在边AB、CD上，且BN＝DM．当点E、F分别在BM、DN上，连接EF，探究三条线段EF、BE、DF之间满足的数量关系，并证明你的结论．
（3）如图，当点E、F分别在对角线BD、边CD上．若FC＝2，则BE的长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于点G，下列结论：①
；②AG=
GC；③BE+DF=EF；④
.其中正确的是（ ）
A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y＝mx2﹣4mx+3m（m＞0）与x轴的交点为A，B，与y轴的交点为C，D为抛物线的顶点．
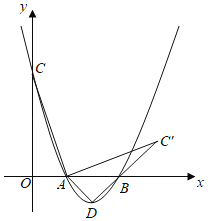
（1）直接写出各点坐标C（ ， ），D（ ， ）；（用m表示）
（2）试说明无论m为何值，抛物线一定经过两个定点并求出这两个定点的坐标；
（3）①将线段AC绕点A顺时针旋转90°得到AC′，求点C′的坐标；
②连接DC'，AD，是否存在m，使得△ADC′为等腰三角形？若存在，请求出m；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中
是直径，点
是上一点，点
是
的中点，过点作的切线，与
、
的延长线分别交于点
、
，连接
.
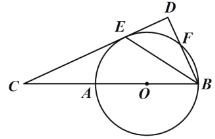
(1)求证：
.
(2)已知的半径为2，当
为何值时，
，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（已知：如图所示的一张矩形纸片ABCD（AD>AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE．
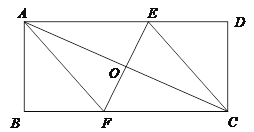
（1）求证：四边形AFCE是菱形；
（2）若AE=10cm，△ABF的面积为24cm2，求△ABF的周长；
（3）在线段AC上是否存在一点P，使得2AE2=AC·AP？若存在，请说明点P的位置，并予以证明；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
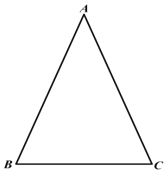
【题目】老师给同学们布置了一个“在平面内找一点，使该点到等腰三角形的三个顶点的距离相等”的尺规作图任务：
下面是小聪同学设计的尺规作图过程：
已知：如图，
中，
，
求作：一点
，使得
.
作法：
①作
的平分线
交
于点
；
②作边
的垂直平分线
，与相交于点；
③连接
，
所以，点就是所求作的点.
根据小聪同学设计的尺规作图过程，
（1）使用直尺和圆规，补全图形（保留作图痕迹）
（2）完成下面的证明.
证明：∵，平分交于点，
∴
是的垂直平分线；（ ）（填推理依据）
∴
.
∵垂直平分，交于点，
∴
；（ ）（填推理依据）
∴.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小王、小张和小梅打算各自随机选择本周六的上午或下午去高邮湖的湖上花海去踏青郊游.
（1）小王和小张都在本周六上午去踏青郊游的概率为_______；
（2）求他们三人在同一个半天去踏青郊游的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（9分）九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：
售价（元/件） | 100 | 110 | 120 | 130 | … |
月销量（件） | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元，设售价为
元．
（1）请用含x的式子表示：①销售该运动服每件的利润是 元；②月销量是 件；（直接写出结果）
（2）设销售该运动服的月利润为
元，那么售价为多少时，当月的利润最大，最大利润是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
