
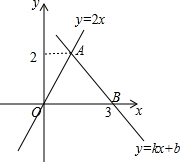 如图,一次函数y=kx+b与正比例函数y=2x的图象交于点A,且与y轴交于点B,则一次函数y=2x-1与y=kx+b的图象交点坐标为($\frac{4}{3}$,$\frac{5}{3}$).
如图,一次函数y=kx+b与正比例函数y=2x的图象交于点A,且与y轴交于点B,则一次函数y=2x-1与y=kx+b的图象交点坐标为($\frac{4}{3}$,$\frac{5}{3}$). 分析 首先由一次函数y=kx+b与正比例函数y=2x的图象交于点A,将y=2代入求得A点坐标,将A,B点坐标代入y=kx+b,可得一次函数解析式,再与y=2x-1联立解方程组可得结果.
解答 解:将y=2代入y=2x,
解得x=1,
所以A(1,2),
将A(1,2),B(3,0)代入y=kx+b可得,
$\left\{\begin{array}{l}{2=k+b}\\{0=3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴一次函数解析式为:y=-x+3,
将y=-x+3与y=2x-1组成方程组,
$\left\{\begin{array}{l}{y=-x+3}\\{y=2x-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=\frac{5}{3}}\end{array}\right.$,
∴交点坐标为($\frac{4}{3}$,$\frac{5}{3}$),
故答案为:($\frac{4}{3}$,$\frac{5}{3}$).
点评 本题主要考查了两直线相交问题,联立方程组解决相交问题是解答此题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com