
| |||||||||||
(1) |
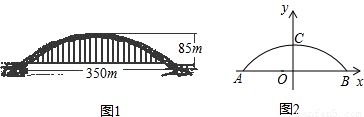
因为桥拱高度OC=85 m,即抛物线过点C(0,85),所以b=85.又由已知得AB=350 m,即点A,B的坐标分别为(-175,0),(175,0),则有0=1752·a+85,解得a≈-0.0028,故所求抛物线的表达式为y=-0.0028x2+85 |
(2) |
解:设DE为水位上升4 m后的桥拱跨度.即当y=4时,有4=-0.002 8x2+85,所以x≈±170,所以D,E两点的坐标分别为(-170,4),(170,4),所以ED≈170+170=340(m). 答:当水位上涨4 m时,位于水面上的桥拱跨度为340 m. 解题指导:此题考查二次函数的图象抛物线及其表达式的相关知识.将题目中所给数据转换成坐标代入函数表达式即可得出结果. |


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:《第26章 二次函数》2009年单元复习测试(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2004年广西南宁市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com