
如图,⊙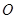 的半径为2,
的半径为2,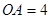 ,
,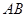 切⊙
切⊙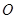 于
于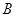 ,弦
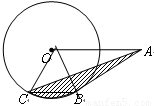
,弦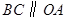 ,连结
,连结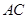 ,图中阴影部分的面积为 .
,图中阴影部分的面积为 .
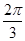
【解析】
试题分析:连接OB、OC,根据切线的性质可得∠ABO=90°,再由OB=2,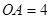 可得∠BAO=30°,则∠AOB=60°,由弦
可得∠BAO=30°,则∠AOB=60°,由弦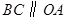 可得△OBC的面积等于△ABC的面积,∠OBC=60°,再结合OB=OC可得∠COB=60°,则阴影部分的面积恰等于圆心角为60°的扇形的面积.
可得△OBC的面积等于△ABC的面积,∠OBC=60°,再结合OB=OC可得∠COB=60°,则阴影部分的面积恰等于圆心角为60°的扇形的面积.
连接OB、OC
∵ 切⊙
切⊙ 于
于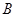
∴∠ABO=90°
∵OB=2,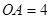
∴∠BAO=30°
∴∠AOB=60°
∵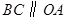
∴△OBC的面积等于△ABC的面积,∠OBC=60°
∵OB=OC
∴∠COB=60°
∴阴影部分的面积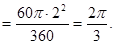
考点:切线的性质,平行线的性质,圆的基本性质,扇形的面积公式
点评:解题的关键是读懂题意及图形,正确作出辅助线,把阴影部分的面积转化为扇形的面积.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
 如图,⊙O的半径为
如图,⊙O的半径为| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com