
����Ŀ����ͼ���߳�Ϊ6�ĵȱ�������ABC�У�D��AB���ϵ�һ���㣬��A��B�˶�(A��B���غ�)��F��BC�ӳ����ϵ�һ���㣬��Dͬʱ����ͬ���ٶ���C��BC�ӳ��߷����˶�(��C���غ�)������D��DE��AC������DF��AC��G��
(1)����D�˶���AB���е�ʱ��ֱ��д��AE�ij���
(2)��DF��ABʱ����AD�ij���
(3)���˶��������߶�GE�ij��Ƿ����仯��������䣬����߶�GE�ij�����������ı���˵�����ɣ�

���𰸡���1��![]() ��2��2 ��3�����䣻3
��2��2 ��3�����䣻3
��������
��1���ɵ�D�˶���AB���е�õ�AD��![]() AB��3�����ݵȱ������ε����ʿɵã���A��60�㣬��á�ADE��30�㣬����ֱ�������ε����ʼ��ɵõ����ۣ�
AB��3�����ݵȱ������ε����ʿɵã���A��60�㣬��á�ADE��30�㣬����ֱ�������ε����ʼ��ɵõ����ۣ�
��2���ɵ�E��Fͬʱ�˶����ٶ���ͬ�õ�AD��CF�������AGD����CGF��30�㣬��F��30�㣬�����õ�CF��CG��AD����AD��CG��CF��x����AG��2x���з��̼�����⣻
��3����FQ��AC�����߶�AC���ӳ����ڵ�Q������FE��DQ����֪AD��CF�����ݵȱ������ε����ʵõ���A����ABC����QCF��60�㣬�̶��Ƴ���ADE�ա�CFQ(AAS)����AE��CQ��DE��QF��DE��QF�ɵ��ı���DEFQ��ƽ���ı��Σ��̶���֪ GE��![]() EQ���Ƴ�GE��
EQ���Ƴ�GE��![]() AC�����ɵõ����ۣ�
AC�����ɵõ����ۣ�
�⣺(1)��D�˶���AB���е�ʱ��
��AD��![]() AB��3����A��60�㣬
AB��3����A��60�㣬
��DE��AC��
���ADE��30�㣬
��AE��![]() AD��
AD��![]() ��
��
(2)�ߵ�D��Fͬʱ�˶����ٶ���ͬ��
��AD��CF��
��DF��AB����A��60�㣬
���AGD����CGF��30�㣬
�ߡ�B��60�㣬
���F��30�㣬
���CGF����F��
��CF��CG��AD��
��AD��CG��CF��x����AG��2x��
��AG+CG��2x+x��3x��6��
��x��2��
��AD��2��
(3)����D��Fͬʱ�˶����ٶ���ͬʱ���߶�GE�ij��Ȳ���ı䣮�������£�
��FQ��AC�����߶�AC���ӳ����ڵ�Q������FE��DQ��
�֡�DE��AB��E��
���GQF����AED��90�㣬
�ߵ�D��F�ٶ���ͬ��
��AD��CF��
�ߡ�ABC�ǵȱ������Σ�
���A����ABC����QCF��60�㣬
�ڡ�ADE�͡�CFQ�У�
�ߡ�AED����CQF��90�㣬
���AED����CQF��

�ڡ�ADE�͡�CQF��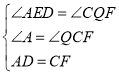 ��
��
���ADE�ա�CFQ(AAS)��
��AE��CQ��DE��QF��DE��QF��
���ı���DEFQ��ƽ���ı��Σ�
��GE��![]() EQ��
EQ��
��EC+AE��CE+CQ��AC��
��GE��![]() AC��
AC��
�֡ߵȱߡ�ABC�ı߳�Ϊ6��
��GE��3��
���D��Fͬʱ�˶����ٶ���ͬʱ���߶�GE�ij��Ȳ���ı䣮


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֪ʶ�������dz�����ѧ��һ����Ҫ���ߣ�����������Խ������������ؽ� ��.�о��������Ƿ�����������Ҫ�Ĺ��ɣ��������ϵ� A���� B ��ʾ�����ֱ�Ϊ a��b����A��B ����֮��ľ��� AB= ![]() ���߶� AB ���е��ʾ����Ϊ
���߶� AB ���е��ʾ����Ϊ![]() .
.
�������龳����ͼ�������ϵ�A��ʾ����Ϊ-2����B��ʾ����Ϊ8����P�ӵ� A ������ ��ÿ��3����λ���ȵ��ٶ����������������˶���ͬʱ��Q�ӵ�B��������ÿ�� 2���� λ���ȵ��ٶ����������˶������˶�ʱ��Ϊt��(t��0).
���ۺ����á�(1) ��գ�
��A��B����֮��ľ���AB=__________���߶�AB���е��ʾ����Ϊ_______��
���ú�t�Ĵ���ʽ��ʾ��t���P��ʾ����Ϊ_______����Q��ʾ����Ϊ_____.
(2) ��tΪ��ֵʱ��P��Q ������������д������������ʾ������
(3)��tΪ��ֵʱ��PQ=![]() AB��
AB��
(4)����MΪPA���е㣬��NΪPB���е㣬�� P���˶������У��߶�MN�ij����Ƿ� ���仯�����仯����˵�����ɣ������䣬������߶�MN�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�Լ��Դ��ij���п�չ�˽�Լˮ������֪�ó��й���10000����ͥ���ǰ��ij����С�������ȡ�˲��ּ�ͥÿ�µ�ˮ��ѵĿ�֧(��λ��Ԫ),�������ͼ��ʾƵ��ֱ��ͼ(ÿһ�麬ǰһ���߽�ֵ,������һ���߽�ֵ)������ٴε�����Щ��ͥÿ�µ�ˮ��ѵĿ�֧����������ʾ��

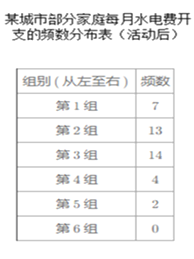
(1)������ȡ��������������
(2)����ÿ��ˮ��ѿ�֧��225Ԫ����(����)Ϊ�ﵽ��Լ��������ͨ�����λ���ó��д�Լ�����˶��ٻ���ͥ�ﵽ��Լ��?
(3)�����Щ������ͥÿ��ˮ��ѿ�֧���ܶ��ܷ����6000Ԫ?
(4)��ѡ��һ���ʵ���ͳ���������ǰ���������ݣ������۽�Լˮ����Ч��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA����5��1����B����2��2����C����1��4�����밴����Ҫ��ͼ��
��1������ABC������ƽ��4����λ���ȡ�������ƽ��1����λ���ȣ��õ���A1B1C1��������A1B1C1��
��2���������ABC����ԭ��O�����ĶԳƵġ�A2B2C2����ֱ��д����A2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϣ���A��ʾ��10����B��ʾ11����C��ʾ18������P�ӵ�A��������������������ÿ��2����λ���ٶ������˶���ͬʱ������Q�ӵ�C�����������Ḻ������ÿ��1����λ���ٶ������˶������˶�ʱ��Ϊt�룮
��1����tΪ��ֵʱ��P��Q����������������M����Ӧ�����Ƕ��٣�
��2���ڵ�Q�������B֮ǰ����tΪ��ֵʱ����P����O�ľ������Q����B�ľ�����ȣ�
��3���ڵ�P�����˶��Ĺ����У�N��AP���е㣬�ڵ�P�����C֮ǰ����2CN��PC��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������a��b�������ϵĶ�Ӧ����ͼ��ʾ��
��1����֪a=�C2.3��b=0.4������|a+b|�C|a|�C|1�Cb|��ֵ��
��2����֪������a��b������|a+b|�C|a|�C|1�Cb|��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���C=120�㣬AD=2AB=4����H��G�ֱ��DZ�CD��BC�ϵĶ��㣮����AH��HG����EΪAH���е㣬��FΪGH���е㣬����EF����EF�����ֵ����Сֵ�IJ�Ϊ�� ��

A. 1 B. ![]() ��1 C.
��1 C. ![]() D. 2��
D. 2��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ������
������![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ��������
ͬʱ��������![]() ��2����/����ٶ����յ�
��2����/����ٶ����յ�![]() �ƶ�����
�ƶ�����![]() ��1����/����ٶ���
��1����/����ٶ���![]() �ƶ�������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶���ʱ��Ϊ
�ƶ�������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶���ʱ��Ϊ![]() �룬��
�룬��![]() ________ʱ���Ե�
________ʱ���Ե�![]() ��
��![]() ��
��![]() Ϊ������������ǵ��������Σ�
Ϊ������������ǵ��������Σ�
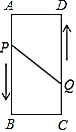
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�и��������������⣺
![]()
��1���������ͼ��A��B�����λ�ã��ֱ�д����������ʾ��������Ϊ��������������
��2���۲����ᣬ���A�ľ���Ϊ4�ĵ��ʾ��������������������
��3������������۵���ʹ�õ�A���ʾ��2�ĵ��غϣ����B���ʾ���������������ĵ��غϣ�
��4�����������M��N����֮��ľ���Ϊ2020��M��N����ࣩ����M��N���㾭����3�����۵������غϣ���M��N��������ʾ�����ֱ�����������������������![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com