
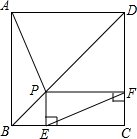
 如图所示,点P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列四个结论:
如图所示,点P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列四个结论:| 2 |
| 2 |
 解:如图,连接PC,在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
解:如图,连接PC,在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
|
| 2 |
| 2 |


科目:初中数学 来源:数学教研室 题型:044
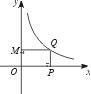
(1)四边形OPQM的面积是多少?
(2)当点P沿x轴的正方向运动时,四边形OPQM的面积有何变化?试述你的理由。
查看答案和解析>>
科目:初中数学 来源:新课程学习手册 数学 八年级(下) 配人教课标版 题型:013
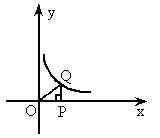
如图所示,点P是x轴正半轴上的一个动点,过点P作x轴的垂线交双曲线y=![]() 于点Q,连接OQ,当点P沿x轴的正方向运动时Rt△QOP的面积
于点Q,连接OQ,当点P沿x轴的正方向运动时Rt△QOP的面积

A.逐渐增大
B.逐渐减小
C.保持不变
D.无法确定
查看答案和解析>>
科目:初中数学 来源:新教材完全解读 八年级数学 (下册) (配人教版新课标) 人教版新课标 题型:013
如图所示,点P是x轴正半轴上的一个动点,过P作x轴的垂线交双曲线y=![]() 于点Q,连接OQ,当点P沿x轴正方向运动时,Rt△QOP的面积
于点Q,连接OQ,当点P沿x轴正方向运动时,Rt△QOP的面积

A.逐渐增大
B.逐渐减小
C.保持不变
D.无法确定
查看答案和解析>>
科目:初中数学 来源:双色笔记九年级数学(上) 题型:013
如图所示,点P是x轴正半轴上的一个动点,过点P作x轴的垂线PQ交双曲线y=![]() 于点Q,连接OQ,当点P沿x轴正方向运动时,Rt△QOP的面积
于点Q,连接OQ,当点P沿x轴正方向运动时,Rt△QOP的面积
[ ]
查看答案和解析>>
科目:初中数学 来源: 题型:013
如图所示,点P是x轴正半轴上的一个动点,过点P作x轴的垂线交双曲线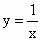 于点Q,连接OQ,当点P沿x轴的正方向运动时,Rt△QOP的面积
于点Q,连接OQ,当点P沿x轴的正方向运动时,Rt△QOP的面积
[ ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com