【题目】已知，如图，在平面直角坐标系中，直线
分别与
轴交于
与反比例函数的图象交于点
，
轴于点
，
.
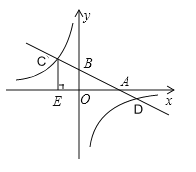
（1）求反比例函数及一次函数的解析式.
（2）当
为何值时一次函数的值大于反比例函数的值.
【答案】（1）见解析；（2）见解析.
【解析】
（1）根据
可求出点A、B、C的坐标，然后用待定系数法求出反比例函数及一次函数的解析式即可；
（2）联立反比例函数解析式和一次函数解析式求出点D坐标，然后根据函数图像和交点坐标即可求得.
解：（1）
，
，
轴于点
，
∴
，
，
，
，
，
设反比例函数解析式为：
，将点代入可得：k=-6，
即反比例函数解析式为：
，
设一次函数解析式为：y=kx+b(k≠0)，将，代入可得：
，
解得：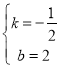
，
即一次函数解析式为：y=
；
（2）联立反比例函数解析式和一次函数解析式可得：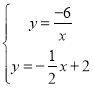
，
解得：
或
，
∴D(6，-1)，
由图像得：一次函数的值大于反比例函数的值时x的取值范围是：x＜-2或0＜x＜6.
一诺书业暑假作业快乐假期云南美术出版社系列答案科目：初中数学 来源： 题型：
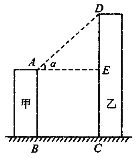
【题目】如图所示．线段AB、DC分别表示甲、乙两座建筑物的高．AB⊥BC，DC⊥BC，两建筑物间距离BC＝30米，若甲建筑物高AB＝28米，在A点测得D点的仰角α＝45°，则乙建筑物高DC＝______米．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，∠C＝90°，BC＝3，AC＝4，BD平分∠ABC，将△ABC绕着点A旋转后，点B、C的对应点分别记为B1、C1，如果点B1落在射线BD上，那么CC1的长度为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，A、B、C是直线l上的三个点，∠DAB＝∠DBE＝∠ECB＝a，且BD＝BE．
（1）求证：AC＝AD+CE；
（2）若a＝120°，点F在直线l的上方，△BEF为等边三角形，补全图形，请判断△ACF的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
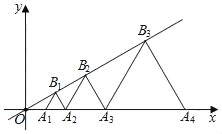
【题目】如图，直线OD与x轴所夹的锐角为30°，OA1的长为1，△A1A2B1、△A2A3B2、△A3A4B3、…、△AnAn+1Bn均为等边三角形，点A1、A2、A3、…、An+1在x轴的正半轴上依次排列，点B1、B2、B3、…、Bn在直线OD上依次排列，那么B2019的坐标为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们约定，在平面直角坐标系中两条抛物线有且只有一个交点时，我们称这两条抛物线为“共点抛物线”，这个交点为“共点”．
（1）判断抛物线y＝x2与y＝﹣x2是“共点抛物线”吗？如果是，直接写出“共点”坐标；如果不是，说明理由；
（2）抛物线y＝x2﹣2x与y＝x2﹣2mx﹣3是“共点抛物线”，且“共点”在x轴上，求抛物线y＝x2﹣2mx﹣3的函数关系式；
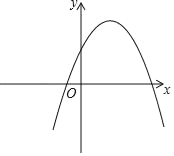
（3）抛物线L1：y＝﹣x2+2x+1的图象如图所示，L1与L2：y＝﹣2x2+mx是“共点抛物线”；
①求m的值；
②点P是x轴负半轴上一点，设抛物线L1、L2的“共点”为Q，作点P关于点Q的对称点P′，以PP′为对角线作正方形PMP′N，当点M或点N落在抛物线L1上时，直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】鲜丰水果店计划用
元/盒的进价购进一款水果礼盒以备销售.
据调查，当该种水果礼盒的售价为
元/盒时，月销量为
盒，每盒售价每增长
元，月销量就相应减少
盒，若使水果礼盒的月销量不低于
盒，每盒售价应不高于多少元?
在实际销售时，由于天气和运输的原因，每盒水果礼盒的进价提高了
，而每盒水果礼盒的售价比(1)中最高售价减少了
，月销量比(1)中最低月销量盒增加了
，结果该月水果店销售该水果礼盒的利润达到了
元，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】深圳某学校为构建书香校园，拟购进甲、乙两种规格的书柜放置新购置的图书．已知每个甲种书柜的进价比每个乙种书柜的进价高20%，用3600元购进的甲种书柜的数量比用4200元购进的乙种书柜的数量少4台．
（1）求甲、乙两种书柜的进价；
（2）若该校拟购进这两种规格的书柜共60个，其中乙种书柜的数量不大于甲种书柜数量的2倍．请您帮该校设计一种购买方案，使得花费最少．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
