
已知一次函数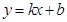 的图象经过点
的图象经过点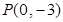 ,且与函数
,且与函数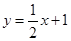 的图象相交于点
的图象相交于点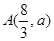 .
.
(1)求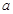 的值;
的值;
(2)若函数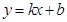 的图象与
的图象与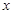 轴的交点是B,函数
轴的交点是B,函数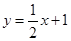 的图象与
的图象与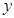 轴的交点是C,求四边形
轴的交点是C,求四边形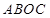 的面积(其中O为坐标原点).
的面积(其中O为坐标原点).
(1)a=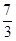 ;(2)SABOC=
;(2)SABOC=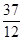 .
.
【解析】
试题分析:(1)根据一次函数y=kx+b的图象与函数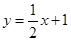 的图象相交于点
的图象相交于点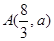 ,先求a的值,
,先求a的值,
(2)再把A、P两点的坐标代入一次函数y=kx+b中,求得k、b的值,再由题意求得B、C两点的坐标,从而求出四边形ABOC的面积
试题解析:
(1)由题意将A坐标代入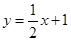 得:a=
得:a=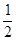 ×
×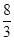 +1=
+1=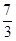
(2)∵直线y=kx+b过点P(0,−3),A(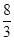 ,
,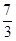 ),
),
∴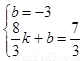 ,解得
,解得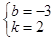
∴函数y=2x-3的图象与x轴的交点B(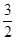 ,0)
,0)
函数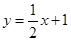 的图象与y轴的交点C(0,1)
的图象与y轴的交点C(0,1)
又S△ACP=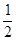 ×4×
×4×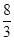 =
=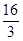 ,S△BOP=
,S△BOP=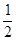 ×3×
×3×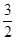 =
=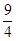 ,(7分)
,(7分)
∴SABOC=S△ACP−S△BOP=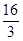 −
−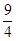 =
=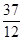 .(8分)
.(8分)
考点:一次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 1 |
| 20k |
| k+1 |
| 1-k |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
先阅读,然后解决问题:
已知:一次函数![]() 和反比例函数
和反比例函数![]() ,求这两个函数图象在同一坐标系内的交点坐标。
,求这两个函数图象在同一坐标系内的交点坐标。
解:解方程-x+2=![]()
去分母,得
-x2+2x=-8
整理得
x2-2x-8=0
解这个方程得:x1=-2 x2=4
经检验,x1=-2 x2=4是原方程的根
当x1=-2,y1=4;x2=4,y2=-2
∴交点坐标为(-2,4)和(4,-2)
问题:
1.在同一直角坐标系内,求反比例函数y= 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标;
2.判断一次函数y=2x-3的图象与反比例函数y=-![]() 的图象在同一直角坐标系内有无交点,说明理由.
的图象在同一直角坐标系内有无交点,说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省九年级上学期期中数学卷 题型:解答题
先阅读,然后解决问题:
已知:一次函数 和反比例函数
和反比例函数 ,求这两个函数图象在同一坐标系内的交点坐标。
,求这两个函数图象在同一坐标系内的交点坐标。
解:解方程-x+2=
去分母,得
-x2+2x=-8
整理得
x2-2x-8=0
解这个方程得:x1=-2 x2=4
经检验,x1=-2 x2=4是原方程的根
当x1=-2,y1=4;x2=4,y2=-2
∴交点坐标为(-2,4)和(4,-2)
问题:
1.在同一直角坐标系内,求反比例函数y= 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标;
2.判断一次函数y=2x-3的图象与反比例函数y=- 的图象在同一直角坐标系内有无交点,说明理由.
的图象在同一直角坐标系内有无交点,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com