
【题目】下列说法不正确的是( )
A.为了解全市中小学生对网络直播课的满意程度,应采用抽样调查
B.数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的方差为
的方差为![]()
C.三角形的的内心到三角形三边距离相等
D.顺次连接对角线垂直的四边形的中点,所形成的四边形为菱形
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为C(0,![]() ),与x轴交于A、B两点,且A(﹣1,0).
),与x轴交于A、B两点,且A(﹣1,0).
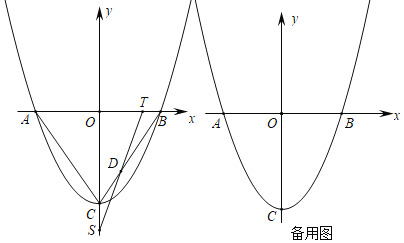
(1)求抛物线的解析式;
(2)点P从点B出发,以每秒1个单位的速度向点A运动,同时点Q从点C出发,以每秒v个单位的速度向y轴负方向匀速运动,运动时间为t秒,连接PQ交射线BC于点D,当点P到达点A时,点Q停止运动,以点P为圆心,PB为半径的圆与射线BC交于点E.
①求BE的长;当t=1时,求DE的长;
②若在点P,Q运动的过程中,线段DE的长始终是一个定值,求v的值及DE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,如果点![]() 到直线
到直线![]() 的距离与它到
的距离与它到![]() 轴、
轴、![]() 轴的距离都相等,那么称点
轴的距离都相等,那么称点![]() 为直线
为直线![]() 的“稳定点”.
的“稳定点”.
(1)到![]() 轴、
轴、![]() 轴的距离相等的点一定在直线__________________上;
轴的距离相等的点一定在直线__________________上;
(2)在下图中作出直线![]() ,并求出该直线所有“稳定点”的坐标;
,并求出该直线所有“稳定点”的坐标;
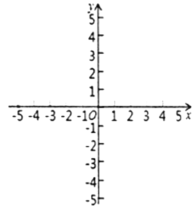
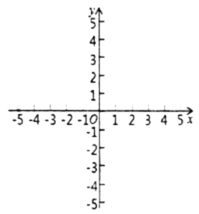
(备用图)
(3)当![]() 时,直线
时,直线![]() 的“稳定点”
的“稳定点”![]() 的坐标为__________________;
的坐标为__________________;
(4)当![]() 时,直线
时,直线![]() 的所有“稳定点”的横坐标之间存在何种数量关系,请画图直接说明,无需证明.
的所有“稳定点”的横坐标之间存在何种数量关系,请画图直接说明,无需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
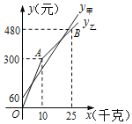
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为x(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与x之间的函数关系如图所示,折线OAB表示y乙与x之间的函数关系.
(1)甲采摘园的门票是 元,乙采摘园优惠前的草莓单价是每千克 元;
(2)当x>10时,求y乙与x的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区![]() 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
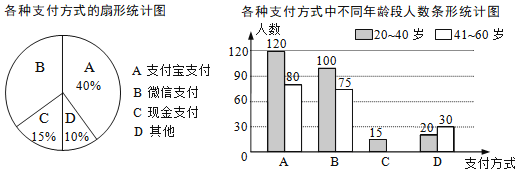
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中![]() 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的一个动点,点
的一个动点,点![]() 是线段
是线段![]() 上的点,
上的点,![]() ,连接
,连接![]() 将
将![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() 为直角三角形,则
为直角三角形,则![]() 为________.
为________.
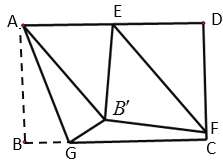
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点![]() 和点
和点![]() 给出如下定义:若
给出如下定义:若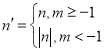 ,则称点
,则称点![]() 为点
为点![]() 的绝对点.例如:点
的绝对点.例如:点![]() 的绝对点坐标是
的绝对点坐标是![]() ,点
,点![]() 的绝对点坐标是
的绝对点坐标是![]() .
.
(1)点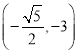 的绝对点坐标是_______.
的绝对点坐标是_______.
(2)若点![]() 在函数
在函数![]()
![]() 的图像上,其绝对点
的图像上,其绝对点![]() 的纵坐标
的纵坐标![]() 的取值范围为
的取值范围为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若点![]() 在关于
在关于![]() 的二次函数
的二次函数![]() 图像上,其绝对点
图像上,其绝对点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() 或
或![]() ,其中
,其中![]() ,令
,令![]() ,是否存在
,是否存在![]() 使得
使得![]() 有最大值,若有请求出
有最大值,若有请求出![]() 的最大值及此时
的最大值及此时![]() 的值;若无,请说明理由.
的值;若无,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°,求建筑物CD的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在∠DAM内部做Rt△ABC,AB平分∠DAM,∠ACB=90°,AB=10,AC=8,点N为BC的中点,动点E由A点出发,沿AB运动,速度为每秒5个单位,动点F由A点出发,沿AM运动,速度为每秒8个单位,当点E到达点B时,两点同时停止运动,过A、E、F作⊙O.
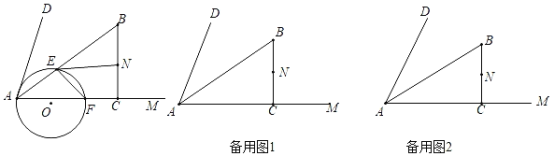
(1)判断△AEF的形状为 ,并判断AD与⊙O的位置关系为 ;
(2)求t为何值时,EN与⊙O相切,求出此时⊙O的半径,并比较半径与劣弧![]() 长度的大小;
长度的大小;
(3)直接写出△AEF的内心运动的路径长为 ;(注:当A、E、F重合时,内心就是A点)
(4)直接写出线段EN与⊙O有两个公共点时,t的取值范围为 .
(参考数据:sin37°=![]() ,tan37°=
,tan37°=![]() ,tan74°≈
,tan74°≈![]() ,sin74°≈
,sin74°≈![]() ,cos74°≈
,cos74°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com