
°æƒø°øœ÷”–Àƒ∏ˆÕ‚π€”Î÷ µÿÕÍ»´œýÕ¨µƒ–°«Ú£¨–°«Ú…œ∑÷±±Í”– ˝◊÷![]() £ÆΩ´Àƒ∏ˆ–°«Ú∑≈÷√”⁄≤ªÕ∏√˜µƒ∫–◊”÷–£¨“°‘»∫Û£¨º◊¥”÷–Àʪ˙≥È»°“ª∏ˆ–°«Ú£¨º«¬º ˝◊÷∫Û∑≈ªÿ“°‘»£¨““‘ŸÀʪ˙≥È»°“ª∏ˆ£Æ
£ÆΩ´Àƒ∏ˆ–°«Ú∑≈÷√”⁄≤ªÕ∏√˜µƒ∫–◊”÷–£¨“°‘»∫Û£¨º◊¥”÷–Àʪ˙≥È»°“ª∏ˆ–°«Ú£¨º«¬º ˝◊÷∫Û∑≈ªÿ“°‘»£¨““‘ŸÀʪ˙≥È»°“ª∏ˆ£Æ
£®1£©«Î”√¡–±Ì∑®ªÚª≠ ˜◊¥Õºµƒ∑Ω∑®£¨«Û¡Ω»À≥È»°œýÕ¨ ˝◊÷µƒ∏≈¬ £Æ
£®2£©»Ù¡Ω»À≥È»°µƒ ˝◊÷∫ÕŒ™![]() µƒ±∂ ˝£¨‘Úº◊ªÒ §£ª»Ù≥È»°µƒ ˝◊÷∫ÕŒ™
µƒ±∂ ˝£¨‘Úº◊ªÒ §£ª»Ù≥È»°µƒ ˝◊÷∫ÕŒ™![]() µƒ±∂ ˝£¨‘Ú““ªÒ §£¨∑Ò‘ÚŒ™∆Ωæ÷£Æ’‚∏ˆ”Œœ∑π´∆Ω¬£ø«Î”√À˘—ßµƒ∏≈¬ µƒ÷™ ∂º”“‘Ω‚ Õ£Æ
µƒ±∂ ˝£¨‘Ú““ªÒ §£¨∑Ò‘ÚŒ™∆Ωæ÷£Æ’‚∏ˆ”Œœ∑π´∆Ω¬£ø«Î”√À˘—ßµƒ∏≈¬ µƒ÷™ ∂º”“‘Ω‚ Õ£Æ
°æ¥∞∏°ø£®1£©Õº±Ìº˚Ω‚Œˆ£¨![]() £ª£®2£©≤ªπ´∆Ω£¨¿Ì”…º˚Ω‚Œˆ
£ª£®2£©≤ªπ´∆Ω£¨¿Ì”…º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©œ»”√¡–±Ì∑®¡–≥ˆÀ˘”–ø…ƒÐµƒΩ·π˚£¨‘Ÿ«Û∏≈¬ £Æ
£®2£©±»Ωœ¡Ω÷÷Ω·π˚µƒ∏≈¬ º¥ø…«ÛΩ‚£Æ
Ω‚£∫![]() ¡–±Ì»Áœ¬
¡–±Ì»Áœ¬
º◊ ““ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥”±Ì∏Òø…“‘ø¥≥ˆ£¨◊Ðπ≤”–![]() ÷÷Ω·π˚£¨√ø÷÷Ω·π˚≥ˆœ÷µƒø…ƒÐ–‘œýÕ¨£¨∆‰÷–¡Ω»À≥È»°œýÕ¨ ˝◊÷µƒΩ·π˚”–
÷÷Ω·π˚£¨√ø÷÷Ω·π˚≥ˆœ÷µƒø…ƒÐ–‘œýÕ¨£¨∆‰÷–¡Ω»À≥È»°œýÕ¨ ˝◊÷µƒΩ·π˚”–![]() ÷÷£¨
÷÷£¨
À˘“‘¡Ω»À≥È»°œýÕ¨ ˝◊÷µƒ∏≈¬ Œ™![]()
![]() ≤ªπ´∆Ω£Æ
≤ªπ´∆Ω£Æ
¥”![]() ÷–±Ì∏Òø…“‘ø¥≥ˆ£¨¡Ω»À≥È»° ˝◊÷∫ÕŒ™
÷–±Ì∏Òø…“‘ø¥≥ˆ£¨¡Ω»À≥È»° ˝◊÷∫ÕŒ™![]() µƒ±∂ ˝µƒΩ·π˚”–
µƒ±∂ ˝µƒΩ·π˚”–![]() ÷÷£¨¡Ω»À≥È»° ˝◊÷∫ÕŒ™
÷÷£¨¡Ω»À≥È»° ˝◊÷∫ÕŒ™![]() µƒ±∂ ˝µƒΩ·π˚”–
µƒ±∂ ˝µƒΩ·π˚”–![]() ÷÷£¨
÷÷£¨
À˘“‘º◊ªÒ §µƒ∏≈¬ Œ™![]() £¨““ªÒ §µƒ∏≈¬ Œ™
£¨““ªÒ §µƒ∏≈¬ Œ™![]()
![]()
![]() º◊ªÒ §µƒ∏≈¬ ¥Û£¨”Œœ∑≤ªπ´∆Ω£Æ
º◊ªÒ §µƒ∏≈¬ ¥Û£¨”Œœ∑≤ªπ´∆Ω£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
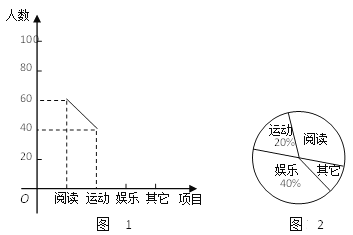
°æƒø°øƒ≥÷–—ßÕ≈ŒØª·Œ™—–æø∏√–£—ß…˙µƒøŒ”ýªÓ∂Ø«Èøˆ£¨≤…»°≥È—˘µƒ∑Ω∑®£¨¥”‘ƒ∂¡°¢‘À∂Ø°¢”È¿÷°¢∆‰À¸µ»Àƒ∏ˆ∑Ω√ʵ˜≤È¡À»Ù∏…√˚—ß…˙µƒ–À»§∞Æ∫√£¨≤¢Ω´µ˜≤ȵƒΩ·π˚ªÊ÷∆¡À»Áœ¬µƒ¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£®»ÁÕº1£¨Õº2£©£¨«Îƒ„∏˘æðÕº÷–Ã·π©µƒ–≈œ¢Ω‚¥œ¬¡–Œ £∫
£®1£©‘⁄’‚¥Œ—–æø÷–£¨“ªπ≤µ˜≤È¡À∂ý…Ÿ√˚—ß…˙£ø
£®2£©°∞∆‰À¸°±‘⁄…»–ŒÕº÷–À˘’ºµƒ‘≤–ƒΩ« «∂ý…Ÿ∂»£ø
£®3£©≤π»´∆µ ˝∑÷≤º’€œþÕº£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
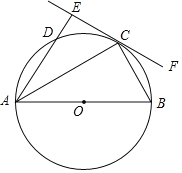
°æƒø°ø»ÁÕº£¨ABŒ™°—Oµƒ÷±æ∂£¨C£¨DŒ™°—O…œµƒ¡Ωµ„£¨°œBAC£Ω°œDAC£¨π˝µ„C◊ˆ÷±œþEF°ÕAD£¨ΩªADµƒ—”≥§œþ”⁄µ„E£¨¡¨Ω”BC£Æ
£®1£©«Û÷§£∫EF «°—Oµƒ«–œþ£Æ
£®2£©»Ù°œCAO£Ω30°„£¨BC£Ω2£¨«Û¡”ª°BCµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨![]() °¢
°¢![]() °¢
°¢![]() »˝µ„µƒ◊¯±Í∑÷±Œ™
»˝µ„µƒ◊¯±Í∑÷±Œ™![]() £¨
£¨![]() £¨
£¨![]() £¨µ„
£¨µ„![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() …œµƒ“ª∏ˆ∂ص„£¨¡¨Ω”
…œµƒ“ª∏ˆ∂ص„£¨¡¨Ω”![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() Ωª
Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨µ±µ„
£¨µ±µ„![]() ¥”
¥”![]() ‘À∂صΩ
‘À∂صΩ![]() ±£¨µ„
±£¨µ„![]() ÀÊ÷Æ‘À∂Ø£¨…˵„
ÀÊ÷Æ‘À∂Ø£¨…˵„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨‘Ú
£¨‘Ú![]() µƒ»°÷µ∑∂Œß «_____£Æ
µƒ»°÷µ∑∂Œß «_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥…ú“‘⁄π∫Ω¯“ªøÓ≤˙∆∑ ±£¨”…”⁄‘À ‰≥…±æº∞≤˙∆∑≥…±æµƒÃ·∏þ£¨∏√≤˙∆∑µ⁄ x Ãϵƒ≥…±æ y£®‘™/º˛£©”Î x£®ÃÏ£©÷ƺ‰µƒπÿœµ»ÁÕºÀ˘ 棨≤¢¡¨–¯ 60 ÃÏæ˘“‘ 80 ‘™/º˛µƒº€∏Ò≥ˆ €£¨ µ⁄ x ÃÏ∏√≤˙∆∑µƒœ˙ €¡ø z£®º˛£©”Î x£®ÃÏ£©¬˙◊„πÿœµ Ω z£Ωx+15£Æ
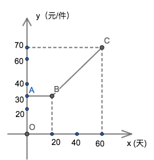
£®1£©µ⁄ 25 ÃÏ£¨∏√…ú“µƒ≥…±æ « ‘™£¨ªÒµ√µƒ¿˚»Û « ‘™£ª
£®2£©…˵⁄ x ÃÏ∏√…ú“≥ˆ €∏√≤˙∆∑µƒ¿˚»ÛŒ™ w ‘™£Æ
¢Ÿ«Û w ”Î x ÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
¢⁄«Û≥ˆµ⁄º∏Ãϵƒ¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷–ª™Œƒ√˜£¨‘¥‘∂¡˜≥§£¨÷–ª™∫∫◊÷£¨‘¢“‚…Óπ„£¨Œ™¡À¥´≥–”≈–„¥´Õ≥ŒƒªØ£¨ƒ≥–£æ≈ƒÍº∂◊È÷Ø600√˚—ß…˙≤Œº”¡À“ª¥Œ°∞∫∫◊÷Ã˝–¥°±¥Û»¸![]() »¸∫Û∑¢œ÷À˘”–≤Œ»¸—ß…˙µƒ≥…º®æ˘≤ªµÕ”⁄60∑÷£¨Œ™¡À∏¸∫√µÿ¡ÀΩ‚±æ¥Œ¥Û»¸µƒ≥…º®∑÷≤º«Èøˆ£¨Àʪ˙≥È»°¡À∆‰÷–»Ù∏…√˚—ß…˙µƒ≥…º®◊˜Œ™—˘±æ£¨≥…º®»Áœ¬£∫
»¸∫Û∑¢œ÷À˘”–≤Œ»¸—ß…˙µƒ≥…º®æ˘≤ªµÕ”⁄60∑÷£¨Œ™¡À∏¸∫√µÿ¡ÀΩ‚±æ¥Œ¥Û»¸µƒ≥…º®∑÷≤º«Èøˆ£¨Àʪ˙≥È»°¡À∆‰÷–»Ù∏…√˚—ß…˙µƒ≥…º®◊˜Œ™—˘±æ£¨≥…º®»Áœ¬£∫
90£¨92£¨81£¨82£¨78£¨95£¨86£¨88£¨72£¨66£¨62£¨68£¨89£¨86£¨93£¨97£¨100£¨73£¨76£¨80£¨77£¨81£¨86£¨89£¨82£¨85£¨71£¨68£¨74£¨98£¨90£¨97£¨100£¨84£¨87£¨73£¨65£¨92£¨96£¨60£Æ
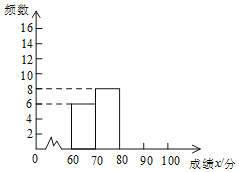
∂‘…œ ˆ≥…º®Ω¯––¡À’˚¿Ì£¨µ√µΩœ¬¡–≤ªÕÍ’˚µƒÕ≥º∆Õº±Ì£∫
≥…º® | ∆µ ˝ | ∆µ¬ |
| 6 |
|
| 8 |
|
| a | b |
| c | d |
«Î∏˘æðÀ˘∏¯–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
![]() ______£¨
______£¨![]() ______£¨
______£¨![]() ______£¨
______£¨![]() ______£ª
______£ª
![]() «Î≤π»´∆µ ˝∑÷≤º÷±∑ΩÕº£ª
«Î≤π»´∆µ ˝∑÷≤º÷±∑ΩÕº£ª
![]() »Ù≥…º®‘⁄90∑÷“‘…œ
»Ù≥…º®‘⁄90∑÷“‘…œ![]() ∞¸¿®90∑÷
∞¸¿®90∑÷![]() µƒŒ™°∞”≈°±µ»£¨«Îƒ„π¿º∆≤Œº”’‚¥Œ±»»¸µƒ600√˚—ß…˙÷–≥…º®°∞”≈°±µ»µƒ‘º”–∂ý…Ÿ»À£ø
µƒŒ™°∞”≈°±µ»£¨«Îƒ„π¿º∆≤Œº”’‚¥Œ±»»¸µƒ600√˚—ß…˙÷–≥…º®°∞”≈°±µ»µƒ‘º”–∂ý…Ÿ»À£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘ƒ∂¡œ¬√ʵƒ≤ƒ¡œ£∫
∞¥’’“ª∂®À≥–Ú≈≈¡–◊≈µƒ“ª¡– ˝≥∆Œ™ ˝¡–£¨ ˝¡–÷–µƒ√ø“ª∏ˆ ˝Ω–◊ˆ’‚∏ˆ ˝¡–µƒœÓ£Æ≈≈‘⁄µ⁄“ªŒªµƒ ˝≥∆Œ™µ⁄“ªœÓ£¨º«Œ™![]() £¨≈≈‘⁄µ⁄∂˛Œªµƒ ˝≥∆Œ™µ⁄∂˛œÓ£¨º«Œ™
£¨≈≈‘⁄µ⁄∂˛Œªµƒ ˝≥∆Œ™µ⁄∂˛œÓ£¨º«Œ™![]() £¨“¿¥À¿ýÕ∆£¨≈≈‘⁄µ⁄
£¨“¿¥À¿ýÕ∆£¨≈≈‘⁄µ⁄![]() Œªµƒ ˝≥∆Œ™µ⁄
Œªµƒ ˝≥∆Œ™µ⁄![]() œÓ£¨º«Œ™
œÓ£¨º«Œ™![]() £ÆÀ˘“‘£¨ ˝¡–µƒ“ª∞„–Œ Ωø…“‘–¥≥…£∫
£ÆÀ˘“‘£¨ ˝¡–µƒ“ª∞„–Œ Ωø…“‘–¥≥…£∫![]() £Æ“ª∞„µÿ£¨»Áπ˚“ª∏ˆ ˝¡–¥”µ⁄∂˛œÓ∆£¨√ø“ªœÓ”ÎÀ¸«∞“ªœÓµƒ≤Óµ»”⁄Õ¨“ª∏ˆ≥£ ˝£¨ƒ«√¥’‚∏ˆ ˝¡–Ω–◊ˆµ»≤Ó ˝¡–£¨’‚∏ˆ≥£ ˝Ω–◊ˆµ»≤Ó ˝¡–µƒπ´≤Ó£¨π´≤ÓÕ®≥£”√
£Æ“ª∞„µÿ£¨»Áπ˚“ª∏ˆ ˝¡–¥”µ⁄∂˛œÓ∆£¨√ø“ªœÓ”ÎÀ¸«∞“ªœÓµƒ≤Óµ»”⁄Õ¨“ª∏ˆ≥£ ˝£¨ƒ«√¥’‚∏ˆ ˝¡–Ω–◊ˆµ»≤Ó ˝¡–£¨’‚∏ˆ≥£ ˝Ω–◊ˆµ»≤Ó ˝¡–µƒπ´≤Ó£¨π´≤ÓÕ®≥£”√![]() ±Ì æ£Æ»Á£∫ ˝¡–1£¨3£¨5£¨7£¨°≠Œ™µ»≤Ó ˝¡–£¨∆‰÷–
±Ì æ£Æ»Á£∫ ˝¡–1£¨3£¨5£¨7£¨°≠Œ™µ»≤Ó ˝¡–£¨∆‰÷–![]() £¨π´≤ÓŒ™
£¨π´≤ÓŒ™![]() £Æ
£Æ
∏˘æð“‘…œ≤ƒ¡œ£¨Ω‚¥œ¬¡–Œ £∫
£®1£©µ»≤Ó ˝¡–4£¨7£¨10£¨°≠µƒπ´≤Ó![]() Œ™_______£¨µ⁄6œÓ «_______£ª
Œ™_______£¨µ⁄6œÓ «_______£ª
£®2£©»Áπ˚“ª∏ˆ ˝¡–![]() «µ»≤Ó ˝¡–£¨«“π´≤ÓŒ™
«µ»≤Ó ˝¡–£¨«“π´≤ÓŒ™![]() £¨ƒ«√¥∏˘æð∂®“Âø…µ√µΩ£∫
£¨ƒ«√¥∏˘æð∂®“Âø…µ√µΩ£∫![]() £Æ
£Æ
À˘“‘
![]() £ª
£ª
![]() £ª
£ª
![]() £ª
£ª
°≠°≠
”…¥À£¨«Îƒ„ÃÓø’ÕÍ≥…µ»≤Ó ˝¡–µƒÕ®œÓπ´£∫![]() £ª
£ª
£®3£©![]() «≤ª «µ»≤Ó ˝¡–
«≤ª «µ»≤Ó ˝¡–![]() £¨
£¨![]() £¨
£¨![]() £¨°≠µƒœÓ£ø»Áπ˚ «£¨ «µ⁄º∏œÓ£ø
£¨°≠µƒœÓ£ø»Áπ˚ «£¨ «µ⁄º∏œÓ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø–°ÕıµÁ◊”≤˙∆∑◊®πÒ“‘20‘™/∏±µƒº€∏Ò≈˙∑¢¡Àƒ≥–¬øÓ∂˙ª˙£¨‘⁄ ‘œ˙µƒ60Ãσ⁄’˚¿Ì≥ˆ¡Àœ˙ € ˝æð»Áœ¬
œ˙ € ˝æð(µ⁄xÃÏ) | €º€(‘™) | »’œ˙ €¡ø(∏±) |
1°Ðx£º35 | x+30 | 100©Å2x |
35°Ðx°Ð60 | 70 | 100©Å2x |
(1)»Ù ‘œ˙Ω◊∂Œ√øÃϵƒ¿˚»ÛŒ™W‘™£¨«Û≥ˆW”Îxµƒ∫Ø ˝πÿœµ Ω£ª
(2)«ÎŒ ‘⁄ ‘œ˙Ω◊∂Œµƒƒƒ“ªÃÏœ˙ €¿˚»ÛWø…“‘¥ÔµΩ◊Ó¥Û÷µ£ø◊Ó¥Û÷µŒ™∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() Ωª
Ωª![]() ÷·”⁄
÷·”⁄![]() £¨
£¨![]() ¡Ωµ„£¨Ωª
¡Ωµ„£¨Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £Æ÷±œþ
£Æ÷±œþ![]() æ≠π˝µ„
æ≠π˝µ„![]() £¨
£¨![]() £Æ
£Æ
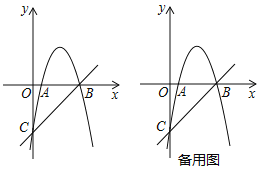
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©π˝µ„![]() µƒ÷±œþΩª÷±œþ
µƒ÷±œþΩª÷±œþ![]() ”⁄µ„
”⁄µ„![]() £Æ
£Æ
¢Ÿµ±![]() ±£¨π˝≈◊ŒÔœþ…œ“ª∂ص„
±£¨π˝≈◊ŒÔœþ…œ“ª∂ص„![]() £®≤ª”ε„
£®≤ª”ε„![]() £¨
£¨![]() ÷ÿ∫œ£©£¨◊˜÷±œþ
÷ÿ∫œ£©£¨◊˜÷±œþ![]() µƒ∆Ω––œþΩª÷±œþ
µƒ∆Ω––œþΩª÷±œþ![]() ”⁄µ„
”⁄µ„![]() £¨»Ù“‘µ„
£¨»Ù“‘µ„![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£¨«Ûµ„
Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£¨«Ûµ„![]() µƒ∫·◊¯±Í£ª
µƒ∫·◊¯±Í£ª
¢⁄¡¨Ω”![]() £¨µ±÷±œþ
£¨µ±÷±œþ![]() ”Î÷±œþ
”Î÷±œþ![]() µƒº–Ω«µ»”⁄
µƒº–Ω«µ»”⁄![]() µƒ
µƒ![]() ±∂ ±£¨«Î÷±Ω”–¥≥ˆµ„
±∂ ±£¨«Î÷±Ω”–¥≥ˆµ„![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com