
 位/秒,2单位/秒的速度移动,同时出发,t表示移动时间(0≤t≤6).
位/秒,2单位/秒的速度移动,同时出发,t表示移动时间(0≤t≤6). AP•AQ=
AP•AQ= •2t(6-t)=-t2+6t,
•2t(6-t)=-t2+6t,
 (6-t)•12+
(6-t)•12+ •2t•6=36,
•2t•6=36, =
=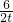 ,
, .
. ,AQ=6-t=
,AQ=6-t= .
. ,0)、Q(0,
,0)、Q(0, )在此直线上,
)在此直线上,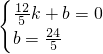 ,
, .
.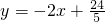 .
. (6-t)•12=36-6t,S△APC=
(6-t)•12=36-6t,S△APC= •2t•6=6t,因此四边形APCQ的面积等于36与t的大小没有关系;
•2t•6=6t,因此四边形APCQ的面积等于36与t的大小没有关系;

 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
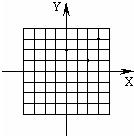 5、已知△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出与△ABC相似(与图形同向),且相似比是3的三角形,它的三个对应顶点的坐标分别是
5、已知△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出与△ABC相似(与图形同向),且相似比是3的三角形,它的三个对应顶点的坐标分别是查看答案和解析>>
科目:初中数学 来源: 题型:
 23、已知△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出△Α1Β1С1与△ABC相似(与图形同向),且相似比是2的三角形,它的三个对应顶点的坐标分别是:
23、已知△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出△Α1Β1С1与△ABC相似(与图形同向),且相似比是2的三角形,它的三个对应顶点的坐标分别是:查看答案和解析>>
科目:初中数学 来源: 题型:
 位/秒,2单位/秒的速度移动,同时出发,t表示移动时间(0≤t≤6).
位/秒,2单位/秒的速度移动,同时出发,t表示移动时间(0≤t≤6).查看答案和解析>>
科目:初中数学 来源:《第24章 图形的相似》2010年兴华学校单元测验题(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com