
(本题8分)
如图,矩形ABCD内接于⊙O,且AB=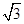 ,BC=1,求图中阴影部分所表示的扇形OAD的面积.
,BC=1,求图中阴影部分所表示的扇形OAD的面积. 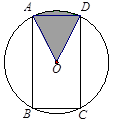
S扇形OAD=
解析 试题分析:∵矩形ABCD内接于⊙O,∴∠B=90o,连结AC。
试题分析:∵矩形ABCD内接于⊙O,∴∠B=90o,连结AC。
∴AC是直径,AC过点O.
Rt△ABC中,AB=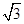 ,BC=1,
,BC=1,
∴,通过勾股定理求出AC=2,扇形OAD的半径R= ="1" ,又∵sin∠BAC=
="1" ,又∵sin∠BAC= ,
,
∴∠BAC=30o,∵AB//DC,∴∠ACD=30o,∴∠AOD=2∠ACD =60o
S扇形OAD=
考点:圆心角与圆周角之间的关系转化
点评:难度较低。本题考查学生对圆心角与圆周角之间的关系转化,通过转化为求圆周角的角度,转化成求直角三角形中其中一个角的角度。利用直角边的边长求正弦值来求角的大小。最后利用扇形面积公式求出答案。学习几何问题后,要能够熟悉各几何图形的各方面计算公式。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013届浙江省乐清市盐盆一中九年级第一次月考数学试卷(带解析) 题型:解答题
(本题10分)如图,矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上,且OD=10,OB=8.将矩形的边BC绕点B逆时针旋转,使点C恰好与x轴上的点A重合.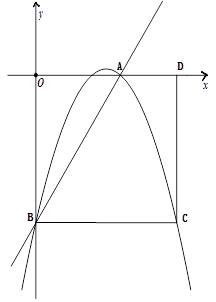
(1)直接写出点A、B的坐标:A( , )、B( , );
(2)若抛物线y=-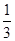 x2+bx+c经过点A、B,请求出这条抛物线的解析式;
x2+bx+c经过点A、B,请求出这条抛物线的解析式;
(3)当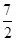 ≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
查看答案和解析>>
科目:初中数学 来源:2011届黑龙江省大庆市三十二中九年级下学期质量检测数学卷 题型:解答题
(本题6分)
如图,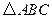 内接于⊙O,点
内接于⊙O,点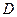 在半径
在半径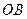 的延长线上,
的延长线上,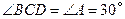 .
.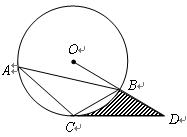
(1)试判断直线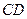 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;
(2)若⊙O的半径长为1,求由弧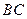 、线段
、线段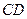 和
和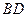 所围成的阴影部分面积(结果保留
所围成的阴影部分面积(结果保留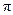 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省镇江市八年级上学期期末考试数学试卷(带解析) 题型:解答题
(本题8分)如图,四边形ABCD是矩形,点O在矩形上方,点B绕着点O逆时针旋转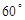 后的对应点为点C.
后的对应点为点C.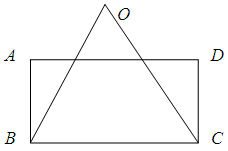
(1)画出点A绕着点O逆时针旋转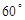 后的对应点E;
后的对应点E;
(2)连接CE,证明:CO平分∠ECD
(3)在(1)(2)的条件下,连接ED,猜想ED与CO的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省乐清市九年级第一次月考数学试卷(解析版) 题型:解答题
(本题10分)如图,矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上,且OD=10,OB=8.将矩形的边BC绕点B逆时针旋转,使点C恰好与x轴上的点A重合.
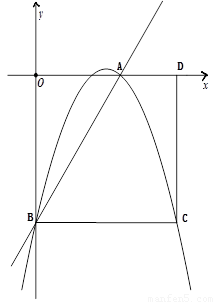
(1)直接写出点A、B的坐标:A( , )、B( , );
(2)若抛物线y=- x2+bx+c经过点A、B,请求出这条抛物线的解析式;
x2+bx+c经过点A、B,请求出这条抛物线的解析式;
(3)当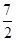 ≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com