【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,4),B(3,2),C(6,3).
(1)画出△ABC关于x轴对称的△A
BC；
(2)以M点为位似中心,在网格中画出△ABC的位似图形△A
BC,使△A2B2C2与△ABC的相似比为2:1.
(3)请写出(2)中放大后的△ABC中AB边的中点P的坐标.
春雨教育同步作文系列答案科目：初中数学 来源： 题型：
【题目】小明练习跳绳，以1分钟跳165个为目标，并把20次1分钟跳绳的数记录如表（超过165个的部分记为“＋”，少于165个的部分记为“－”)
与目标数量的差值 （单位：个） | －12 | －6 | －2 | ＋5 | ＋11 |
次数 | 3 | 5 | 4 | 6 | 2 |
(1)小明在这20次跳绳练习中，1分钟最多跳个?
(2)小明在这20次跳绳练习中，1分钟跳绳个数最多的一次比最少的一次多个?
(3)小明在这20次跳绳练习中，累计跳绳多少个?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一名足球守门员练习折返跑，从球门线出发，向前记作正数，返回记作负数，他的记录如下：（单位：米）+5，-3，+10，-8，-6，+12，-10
（1）守门员最后是否回到了球门线的位置？
（2）在练习过程中，守门员离开球门最远距离是多少米？
（3）守门员全部练习结束后，他共跑了多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在学校组织的知识竞赛中，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，学校将某年级的一班和二班的成绩整理并绘制成如下的统计图：
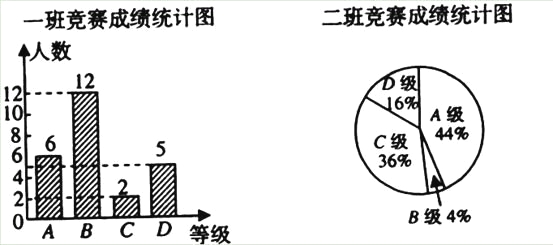
请你根据以上提供的信息解答下列问题：
（1）此次竞赛中二班成绩在C级以上（包括C级）的人数为_______；
（2）请你将表格补充完整：
平均数（分） | 中位数（分） | 众数（分） | |
一班 | 87.6 | 90 | |
二班 | 87.6 | 100 |
（3）请从下列不同角度对这次竞赛成绩的结果进行
①从平均数和中位数的角度来比较一班和二班的成绩；
②从平均数和众数的角度来比较一班和二班的成绩；
③从B级以上（包括B级）的人数的角度来比较一班和二班的成绩．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市某中学开展以“我最喜欢的职业”为主题的调查活动，通过对学生的随机抽样调查得到一组数据，如图是根据这组数据绘制的不完整统计图.
（1）求出被调查的学生人数；
（2）计算并将折线统计图补充完整；
（3）计算扇形统计图中公务员部分对应的圆心角的度数；
（4）若从被调查的学生中任抽一名，求抽取的这名学生最喜欢的职业是“教师”的百分比.
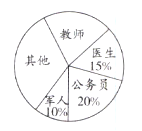
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读以下证明过程：
已知：在△ABC中，∠C≠90°，设AB=c，AC=b，BC=a．求证：a2+b2≠c2．
证明：假设a2+b2=c2，则由勾股定理逆定理可知∠C=90°，这与已知中的∠C≠90°矛盾，故假设不成立，所以a2+b2≠c2．
请用类似的方法证明以下问题：
已知：关于x的一元二次方程x2﹣（m+1）x+2m-3=0 有两个实根x1和x2．
求证：x1≠x2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某登山队3名队员，以1号位置为基地，开始向海拔距基地300m的顶峰冲击，设他们向上走为正，行程记录如下（单位：m）：
+150，﹣35，﹣42，﹣35，+128，﹣26，﹣5，+30，+75
（1）他们最终有没有登上顶峰？如果没有，那么他们离顶峰还差多少米？
（2）登山时，3名队员在进行全程中都使用了氧气，且每人每米要消耗氧气0.04升.他们共使用了氧气多少升？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
