
【题目】已知平行四边形ABCD,连接AF,CE、AF平分![]() 交BC于点F,CE平分
交BC于点F,CE平分![]() 交AD于点E.
交AD于点E.
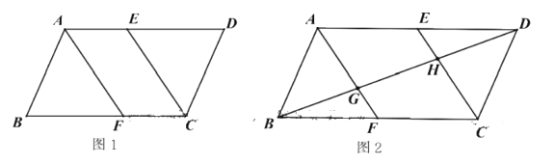
(1)如图1,求证:四边形AFCE为平行四边形;
(2)如图2,连接BD,分别交AF、CE于G、H,若![]() ,在不添加其他辅助线的情况下,直接找出图中面积为平行四边形ABCD面积的
,在不添加其他辅助线的情况下,直接找出图中面积为平行四边形ABCD面积的![]() 的三角形或四边形.
的三角形或四边形.
【答案】(1)详见解析;(2)![]() ,
,![]() ;四边形
;四边形![]() ,四边形
,四边形![]()
【解析】
(1)利用角平分线的性质再结合平行四边形的性质进而得出AF∥EC,即可得出答案;
(2)连接EF,证明E、F分别为AD和BC中点,即可根据三角形面积公式和平行四边形面积公式,知![]() 和
和![]() 面积为行四边形ABCD面积的
面积为行四边形ABCD面积的![]() ;再根据图形的对称性,可知四边形
;再根据图形的对称性,可知四边形![]() 和四边形
和四边形![]() 面积相等,即可得出答案.
面积相等,即可得出答案.
证明:(1)∵AF平分∠BAD,CE平分∠BCD,
∴∠FAE=![]() ∠BAE,∠FCE=
∠BAE,∠FCE=![]() ∠FCD,
∠FCD,
∵四边形ABCD是平行四边形,
∴∠BAE=∠FCD,AD∥BC,
∴∠FAE=∠FCE,∠FCE=∠CED,
∴∠FAE=∠CED,
∴AF∥EC,
又∵AE∥CF,
∴四边形AFCE为平行四边形;
(2)如图,连接EF,

∵AF平分![]() ,
,
∴∠EAF=∠BAF,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠EAF=∠BFA,
∴∠BAF=∠BFA,
∴BA=BF,
∵![]() ,
,
∴BF=FC,即点F为BC的中点,
同理可证点E为AD中点,
∴![]() ,
,
易证四边形![]() ,四边形
,四边形![]() 为全等图形,
为全等图形,
∴![]() ,
,
∴面积为平行四边形ABCD面积的![]() 的三角形或四边形有:
的三角形或四边形有:![]() ,
,![]() ,四边形
,四边形![]() ,四边形
,四边形![]() .
.


科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,武汉市第八十一中学每周三组织开展了社团活动,分别设置了体育、舞蹈、文学、音乐社团(要求人人参与社团,每人只能选择一项),为了解学生喜爱哪种社团活动,学校做了一次抽样调查,根据收集到的数据,绘制成两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
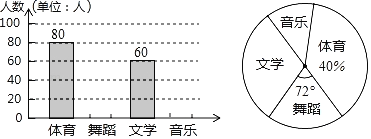
(1)此次共调查了 人,补齐舞蹈社团、音乐社团条形图;
(2)求音乐社团在扇形统计图中所占圆心角的度数 ;
(3)若该校有1600名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查,并绘制成如图①②的统计图。已知“查资料”人人数是40人。
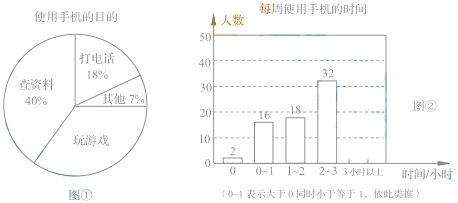
请你根据以上信息解答以下问题
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_______________。
(2)补全条形统计图
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
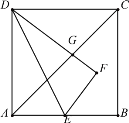
【题目】如图,正方形ABCD的边长为4,E为AB的中点,将△ADE沿直线DE折叠后,点A落在点F处,DF交对角线AC于G,则FG的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() (m>0)与x轴交于A,B两点,点B在点A的右侧,顶点为C,抛物线与y轴交于点D,直线CA交y轴于E,且
(m>0)与x轴交于A,B两点,点B在点A的右侧,顶点为C,抛物线与y轴交于点D,直线CA交y轴于E,且![]() .
.
(1)求点A,点B的坐标;
(2)将△BCO绕点C逆时针旋转一定角度后,点B与点A重合,点O恰好落在y轴上,
①求直线CE的解析式;
②求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
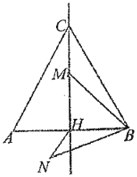
【题目】如图,等边三角形![]() 的边长是2,
的边长是2,![]() 是高
是高![]() 所在直线上的一个动点,连接
所在直线上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,则在点
,则在点![]() 运动过程中,线段
运动过程中,线段![]() 长度的最小值是( )
长度的最小值是( )
A.![]() B.1C.
B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
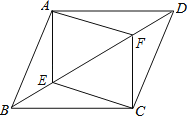
【题目】如图,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.
(1)如果四边形AECF是平行四边形,求证:四边形ABCD也是平行四边形;
(2)如果四边形AECF是菱形,求证:四边形ABCD也是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
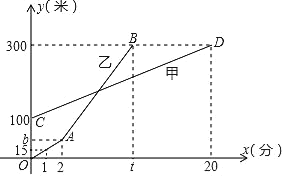
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com