



 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源:不详 题型:解答题
 ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt ABC绕A点顺时针旋转120°后得到Rt
ABC绕A点顺时针旋转120°后得到Rt ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.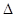 ADE,求出Rt
ADE,求出Rt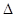 ADE 的直角边DE被⊙M截得的弦PQ的长度;
ADE 的直角边DE被⊙M截得的弦PQ的长度;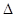 ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
ADE的斜边AD所在的直线与⊙M的位置关系(直接写出答案)
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.(0,0) | B.(1,-1) | C.(2,-1) | D.(3,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com