
【题目】已知(x2+mx+1)(x2﹣2x+n)的展开式中不含x2和x3项.
(1)分别求m、n的值;
(2)化简求值:(m+2n+1)(m+2n﹣1)+(2m2n﹣4mn2+m3)÷(﹣m)
【答案】(1)m的值为2,n的值为3;(2)2mn+8n2﹣1;83.
【解析】
(1)先将题目中的式子化简,然后根据![]() 的展开式中不含
的展开式中不含![]() 和
和![]() 项,可以求得m、n的值;
项,可以求得m、n的值;
(2)先化简题目中的式子,然后将m、n的值代入化简后的式子即可解答本题.
解:(1)![]()
=![]() ﹣2
﹣2![]() +n
+n![]() +m
+m![]() ﹣2m
﹣2m![]() +mnx+
+mnx+![]() ﹣2x+n
﹣2x+n
=![]() +(﹣2+m)
+(﹣2+m)![]() +(n﹣2m+1)
+(n﹣2m+1)![]() +(mn﹣2)x+n,
+(mn﹣2)x+n,
∵![]() 的展开式中不含
的展开式中不含![]() 和
和![]() 项,
项,
∴![]() ,解得
,解得![]() ,
,
即m的值为2,n的值为3;
(2)(m+2n+1)(m+2n﹣1)+(2![]() n﹣4m
n﹣4m![]() +
+![]() )÷(﹣m)
)÷(﹣m)
=[(m+2n)+1][(m+2n)﹣1]﹣2mn+4![]() ﹣
﹣![]()
=![]() ﹣1﹣2mn+4
﹣1﹣2mn+4![]() ﹣
﹣![]()
=![]() +4mn+4
+4mn+4![]() ﹣1﹣2mn+4
﹣1﹣2mn+4![]() ﹣
﹣![]()
=2mn+8![]() ﹣1,
﹣1,
当m=2,n=3时,
原式=2×2×3+8×![]() ﹣1=83.
﹣1=83.
故答案为:(1)m的值为2,n的值为3;(2)2mn+8![]() ﹣1;83.
﹣1;83.


科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
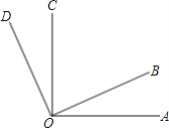
(1)求∠AOD的度数;
(2)∠AOB与∠DOC有何大小关系?
(3)若不知道∠BOC的具体度数,其他条件不变,(2)的关系仍成立吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( ).
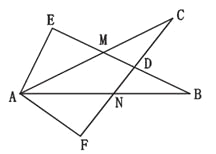
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m﹣2=0.
(1)求证:无论m取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足x12+x22=﹣3x1x2 , 求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,D是AB边上的一动点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:△ACE≌△BCD;
(2)判断AE与BC的位置关系,并说明理由.
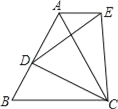
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴和y轴上,OA=3,OB=4.把△AOB绕点A顺时针旋转120°,得到△ADC.边OB上的一点M旋转后的对应点为M′,当AM′+DM取得最小值时,点M的坐标为( )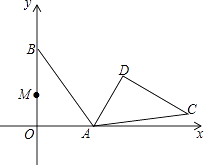
A.(0, ![]() )
)
B.(0, ![]() )
)
C.(0, ![]() )
)
D.(0,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com