
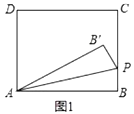
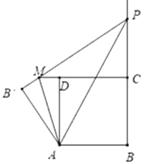
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 出发,以每秒1个单位的速度沿射线
出发,以每秒1个单位的速度沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
(1)当![]() 时.
时.
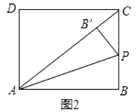
①如图2.当点![]() 落在
落在![]() 上时,显然
上时,显然![]() 是直角三角形,求此时
是直角三角形,求此时![]() 的值;
的值;
②当点![]() 不落在
不落在![]() 上时,请直接写出
上时,请直接写出![]() 是直角三角形时
是直角三角形时![]() 的值;
的值;
(2)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,且当
,且当![]() 时,
时,![]() .问:当
.问:当![]() 时,
时,![]() 的大小是否发生变化,若不变,请说明理由.
的大小是否发生变化,若不变,请说明理由.
【答案】(1)①![]() ,②
,②![]() 或
或![]() 或
或![]() ;(2)不变,见解析
;(2)不变,见解析
【解析】
(1)①利用勾股定理求出AC,再根据折叠的性质以及勾股定理即可得出答案;②分三种情况进行讨论:①如图2-1中,当![]() 时,②如图2-2中,当
时,②如图2-2中,当![]() 时,③如图2-3中,当
时,③如图2-3中,当![]() 时,在
时,在![]() 中分别找出每条边的长度,再利用勾股定理建立方程求解即可得出答案;
中分别找出每条边的长度,再利用勾股定理建立方程求解即可得出答案;
(2)首先证明ABCD是正方形,再利用全等三角形的性质以及折叠的性质即可得出答案.
解:(1)①如图1中,∵四边形![]() 是矩形,
是矩形,
∴![]() ,∴
,∴![]()
∵翻折
∴![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴在![]() 中,
中,![]()
∴![]()
∴![]() ;
;

②如图2-1中,当![]() ,
,![]() 在
在![]() 上时,
上时,
∵四边形![]() 是矩形,∴
是矩形,∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]()
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() .
.
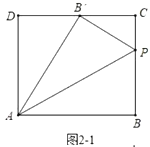
如图2-2中,当![]() ,
,![]() 在
在![]() 的延长线上时,
的延长线上时,
在![]() 中,
中,![]() ,
,
∴![]()
在![]() 中,则有:
中,则有:![]() ,
,
解得![]() .
.
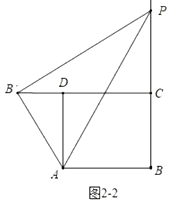
如图2-3中,当![]() 时,
时,
易证四边形![]() 为正方形,则
为正方形,则![]() .
.
综上所述,满足条件的![]() 的值为
的值为![]() 或
或![]() 或
或![]() ;
;

(2)当![]() 时,如图,∵
时,如图,∵![]()
∴![]() ,
,![]()
∵翻折,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即四边形
,即四边形![]() 是正方形,
是正方形,

当![]() 时,如图,设
时,如图,设![]()
∴![]() ,
,
∴![]() ,
,
易证![]() ,
,
∴![]() ,
,
∵翻折,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+![]() =0,
=0,![]()
(1)求C点坐标
(2)作DE DC,交y轴于E点,EF为 AED的平分线,且DFE= 90o。 求证:FD平分ADO;
(3)E 在 y 轴负半轴上运动时,连 EC,点 P 为 AC 延长线上一点,EM 平分∠AEC,且 PM⊥EM,PN⊥x 轴于 N 点,PQ 平分∠APN,交 x 轴于 Q 点,则 E 在运动过程中,![]() 的大小是否发生变化,若不变,求出其值.
的大小是否发生变化,若不变,求出其值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)填空:
①当![]() 的值为_______时,四边形
的值为_______时,四边形![]() 是矩形;
是矩形;
②当![]() 的值为______时,四边形
的值为______时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
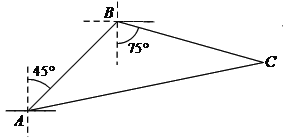
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线![]() 上有
上有![]() 、
、![]() 两个观测站,
两个观测站,![]() 在
在![]() 的正东方向,
的正东方向,![]() (单位:
(单位:![]() )有一艘小船在点
)有一艘小船在点![]() 处,从
处,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,从
的方向,从![]() 测得小船在北偏东
测得小船在北偏东![]() 的方向.(结果保留根号)
的方向.(结果保留根号)
(1)求点![]() 到海岸线
到海岸线![]() 的距离;
的距离;
(2)小船从点![]() 处沿射线
处沿射线![]() 的方向航行一段时间后,到达点
的方向航行一段时间后,到达点![]() 处,此时,从
处,此时,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,求点
的方向,求点![]() 与点
与点![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
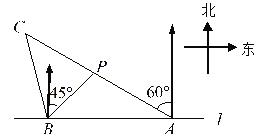
【题目】现有一副直角三角板(角度分别为30°、60°、90°和45°、45°、90°),如图(1)所示,其中一块三角板的直角边AC垂直于数轴,AC的中点过数轴原点O,AC=8,斜边AB交数轴于点G,点G对应数轴上的数是4;另一块三角板的直角边AE交数轴于点F,斜边AD交数轴于点H.
(1)如果△AGH的面积是10,△AHF的面积是8,则点F对应的数轴上的数是 ,点H对应的数轴上的数是 ;
(2)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,若∠HAO=a,试用a来表示∠M的大小:(写出推理过程)
(3)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,设∠EFH的平分线和
∠FOC的平分线交于点N,求∠N+∠M的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() ,
,![]() ,试回答下列问题:
,试回答下列问题:
(1)如图1所示,求证:![]() .
.

(2)如图2,若点![]() 、
、![]() 在
在![]() 上,且满足
上,且满足![]() ,并且
,并且![]() 平分
平分![]() .求
.求![]() ________度.
________度.

(3)在(2)的条件下,若平行移动![]() ,如图3,那么
,如图3,那么![]() 的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(2)的条件下,如果平行移动![]() 的过程中,若使
的过程中,若使![]() ,求
,求![]() 度数.
度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副三角板![]() 和
和![]() 拼合在一起,边
拼合在一起,边![]() 与
与![]() 重合,
重合,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 向下滑动时,点
向下滑动时,点![]() 同时从点
同时从点![]() 出发沿射线
出发沿射线![]() 向右滑动.当点
向右滑动.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,连接
时,连接![]() ,则
,则![]() 的面积最大值为_______
的面积最大值为_______![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com