
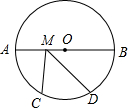
 如图,在⊙O中,AB是⊙O的直径,AB=12,点C、D是$\widehat{AB}$的三等分点,M是AB上一动点,则CM+DM的最小值是( )
如图,在⊙O中,AB是⊙O的直径,AB=12,点C、D是$\widehat{AB}$的三等分点,M是AB上一动点,则CM+DM的最小值是( )| A. | 16 | B. | 12 | C. | 8 | D. | 6 |
分析 作点C关于AB的对称点C′,连接C′D与AB相交于点M,根据轴对称确定最短路线问题,点M为CM+DM的最小值时的位置,根据垂径定理可得$\widehat{AC}$=$\widehat{AC′}$,然后求出C′D为直径,从而得解.
解答 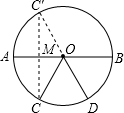 解:如图,作点C关于AB的对称点C′,连接C′D与AB相交于点M,
解:如图,作点C关于AB的对称点C′,连接C′D与AB相交于点M,
此时,点M为CM+DM的最小值时的位置,
由垂径定理,$\widehat{AC}$=$\widehat{AC′}$,
∴$\widehat{BD}$=$\widehat{AC′}$,
∵$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,AB为直径,
∴C′D为直径.
故选B.
点评 本题考查了轴对称确定最短路线问题,垂径定理,熟记定理并作出图形,判断出CM+DM的最小值等于圆的直径的长度是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 实心铁球投入水中会沉入水底 | |
| B. | 抛出一枚硬币,落地后正面向上 | |
| C. | 明天太阳从西边升起 | |
| D. | NBA篮球队员在罚球线投篮2次,至少投中一次 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这1000名考生是总体的一个样本 | B. | 近4万名考生是总体 | ||
| C. | 1000名学生是样本容量 | D. | 每位考生的数学成绩是个体 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com