
 已知,如图,某人站在斜坡端点C处,距离塔底中心B点100米位置,测得塔顶的仰角为60°,又走到坡度为1:2的斜坡P处测得塔顶A的仰角为45°.
已知,如图,某人站在斜坡端点C处,距离塔底中心B点100米位置,测得塔顶的仰角为60°,又走到坡度为1:2的斜坡P处测得塔顶A的仰角为45°.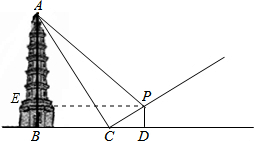
| 3 |
| 3 |
100(
| ||
| 3 |
100(
| ||
| 3 |


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
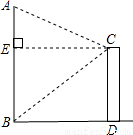
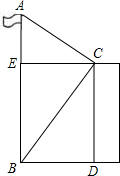 如图,某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到对面旗杆的距离(CE的长度)为10m,测得旗杆顶的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45°,那么AB的高度是( )
如图,某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到对面旗杆的距离(CE的长度)为10m,测得旗杆顶的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45°,那么AB的高度是( )A、(10
| ||||||
B、(10+10
| ||||||
C、(10
| ||||||
D、(10+
|
查看答案和解析>>
科目:初中数学 来源: 题型:
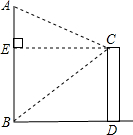 如图,某人站在楼顶观测对面笔直的旗杆AB,已知观测点C到旗杆的距离(CE的长度)为8米,测得旗杆顶的仰角为∠ECA=30°,旗杆底部的俯角∠ECB=45°,那么旗杆AB的高度是
如图,某人站在楼顶观测对面笔直的旗杆AB,已知观测点C到旗杆的距离(CE的长度)为8米,测得旗杆顶的仰角为∠ECA=30°,旗杆底部的俯角∠ECB=45°,那么旗杆AB的高度是查看答案和解析>>
科目:初中数学 来源: 题型:解答题
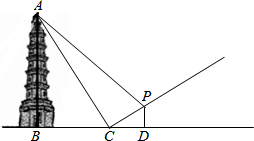 已知,如图,某人站在斜坡端点C处,距离塔底中心B点100米位置,测得塔顶的仰角为60°,又走到坡度为1:2的斜坡P处测得塔顶A的仰角为45°.
已知,如图,某人站在斜坡端点C处,距离塔底中心B点100米位置,测得塔顶的仰角为60°,又走到坡度为1:2的斜坡P处测得塔顶A的仰角为45°.查看答案和解析>>
科目:初中数学 来源:2012年江苏省南通市中考数学模拟试卷(十二)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com